1.(2025·扬州江都区期中)已知关于$x的一元一次方程\frac{1}{2024}x + 3 = 2x + b的解为x = 2$,则关于$y的一元一次方程\frac{1}{2024}(y + 1) + 3 = 2(y + 1) + b$的解为(
A
)。
A.$y = 1$
B.$y = 2$
C.$y = 3$
D.$y = 4$
答案:A [解析]
∵关于x的一元一次方程$\frac{1}{2024}x+3=2x+b$的解为$x=2$,
∴关于y的一元一次方程$\frac{1}{2024}(y+1)+3=2(y+1)+b$的解为$y+1=2$,
∴$y=1$.故选A.
2. 如果$x = -1是方程x + a = 3$的解,则$a = $
4
。
答案:4 [解析]把$x=-1$代入方程,得$-1+a=3$,解得$a=4$.
解析:
把$x = -1$代入方程$x + a = 3$,得$-1 + a = 3$,解得$a = 4$。
4
3. 解方程:
(1)$4x - 2 = 3(2x - 6)$;
(2)$\frac{x + 1}{4} - 1 = \frac{3x - 2}{6}$。
答案:
(1)去括号,得$4x-2=6x-18$,移项,得$4x-6x=-18+2$,合并同类项,得$-2x=-16$,系数化为1,得$x=8$.
(2)去分母,得$3(x+1)-12=2(3x-2)$,去括号,得$3x+3-12=6x-4$,移项,得$3x-6x=-4-3+12$,合并同类项,得$-3x=5$,系数化为1,得$x=-\frac{5}{3}$.
4. 某商店以每盏25元的价格采购了一批节能灯,运输过程中损坏了3盏,然后以每盏30元售完,共获利160元。该商店共购进了多少盏节能灯?
答案:设该商店共购进了x盏节能灯,由题意,得$25x+160=30(x-3)$,解得$x=50$.故该商店共购进了50盏节能灯.
思路引导 本题考查一元一次方程的应用,关键是表示出总进价和总售价,再根据进价、售价、获利情况列出方程求解.
5. 一题多问(2025·苏州相城区期末)平价商场经销甲、乙两种商品,甲种商品每件售价60元,利润率为50%;乙种商品每件进价50元,售价80元。(利润率= (售价-进价)÷进价)
(1)甲种商品每件进价为
40
元,每件乙种商品利润率为
60%
;
(2)若该商场同时购进甲、乙两种商品共50件,恰好总进价为2100元,求购进甲种商品多少件;
设购进甲种商品y件,则购进乙种商品(50-y)件,根据题意,得40y+50(50-y)=2100,解得y=40.故购进甲种商品40件.
(3)在“元旦”期间,该商场对甲、乙两种商品进行如下的优惠促销活动:
|打折前一次性购物总金额|优惠措施|
|少于或等于450元|不优惠|
|超过450元,但不超过600元|按售价打9折|
|超过600元|其中600元部分打8.2折优惠,超过600元的部分打5折优惠|
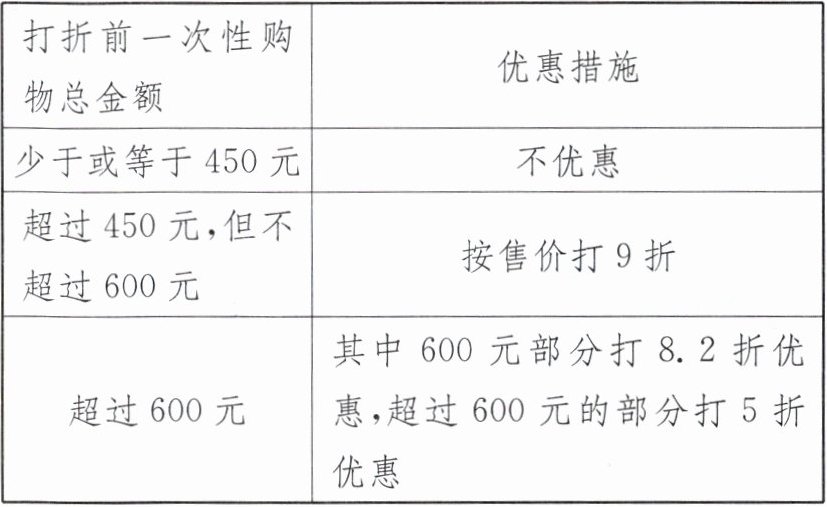
按上述优惠条件,若小华一次性购买乙种商品实际付款592元,求小华在该商场购买乙种商品多少件。
设小华在该商场购买乙种商品m件,∵600×0.9=540(元),540<592,∴小华购买乙种商品打折前总金额超过600元.根据题意,得600×0.82+0.5(80m-600)=592,解得m=10.故小华在该商场购买乙种商品10件.
答案:
(1)40 60% [解析]设甲种商品每件进价为x元,根据题意,得$60-x=50\%x$,解得$x=40$,
∴甲种商品每件进价为40元.每件乙种商品利润率为$\frac{80-50}{50}×100\%=60\%$.
(2)设购进甲种商品y件,则购进乙种商品$(50-y)$件,根据题意,得$40y+50(50-y)=2100$,解得$y=40$.故购进甲种商品40件.
(3)设小华在该商场购买乙种商品m件,
∵$600×0.9=540$(元),$540<592$,
∴小华购买乙种商品打折前总金额超过600元.根据题意,得$600×0.82+0.5(80m-600)=592$,解得$m=10$.故小华在该商场购买乙种商品10件.