1. (2024·唐山一模)一道条件缺失的问题情境:一项工程,甲队单独做需要12天完成……还需要几天完成任务? 根据标准答案,老师在黑板上画出线段示意图(如图),设两队合作还需x天完成任务,并列方程为$\frac{1}{12}×2+(\frac{1}{8}+\frac{1}{12})x= 1$. 根据上面信息,下面结论不正确的是(
D
).
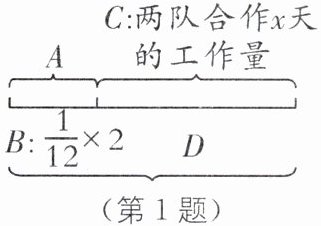
A.乙队单独完成需要8天完成
B.D处代表的代数式$(\frac{1}{8}+\frac{1}{12})x$
C.A处代表的实际意义:甲先做2天的工作量
D.甲先做2天,然后甲、乙两队合作5天完成了整个工程
答案:D
解析:
A. 由方程中$\frac{1}{8}$为乙队工作效率,可得乙队单独完成需8天,正确。
B. 方程中$(\frac{1}{8}+\frac{1}{12})x$表示两队合作$x$天工作量,对应D处,正确。
C. $A$处对应$B:\frac{1}{12}×2$,即甲先做2天工作量,正确。
D. 解方程$\frac{1}{12}×2+(\frac{1}{8}+\frac{1}{12})x=1$,得$x=4$,非5天,错误。
结论不正确的是D。
2. 甲、乙两车从相距280 km的地方相向而行,甲车每小时行驶60 km,乙车每小时行驶80 km,经过多长时间两车相遇?
分析:设x小时后两车相遇.
画出线形示意图如图所示.
根据线形示意图列出相等关系:
60x+80x=280
.

答案:60x+80x=280
解析:
设$x$小时后两车相遇。
$60x + 80x = 280$
$140x = 280$
$x = 2$
答:经过$2$小时两车相遇。
3. 一条公路,从山下到山顶,走了1 h还差1 km,从山顶到山下,用50 min可以走完. 已知下山速度是上山速度的1.5倍,问:下山速度和上山速度各是多少? 单程山路是多长?
答案:设上山速度为x km/h,则下山速度是1.5x km/h,
单程山路是(x+1)km.
根据题意,得x+1=$\frac{5}{6}×1.5x$,解得x=4.
∴下山速度为1.5×4=6(km/h),
单程山路为4+1=5(km).
故上山速度是4 km/h,下山速度是6 km/h,单程山路为5 km.
4. 分类讨论思想 A,B两地相距900 km,一列快车以200 km/h的速度从A地匀速驶往B地,到达B地后立刻原路返回A地,一列慢车以75 km/h的速度从B地匀速驶往A地. 两车同时出发,截止到它们都到达终点时,两车恰好相距200 km的次数是(
A
).
A.5
B.4
C.3
D.2
答案:A [解析]设两车相距200 km时,行驶的时间为t小时,
①当快车从A地开往B地,慢车从B地开往A地,相遇前相距200 km时,
则有200t+75t+200=900,解得t=$\frac{28}{11}$;
②当快车继续开往B地,慢车继续开往A地,相遇后背离而行,相距200 km时,
则有200t+75t-200=900,解得t=4;
③快车从A地到B地全程需要4.5小时,此时慢车从B地到A地行驶4.5×75=337.5(km).
因为337.5 km>200 km,
所以快车又从B地返回A地追慢车,追上前相距200 km,
则有75t=200+200(t-4.5),解得t=$\frac{28}{5}$;
④快车追上慢车后超过慢车相距200 km,
则有200(t-4.5)-75t=200,解得t=$\frac{44}{5}$;
⑤快车返回A地终点所需时间是9小时,此刻慢车行驶了9×75=675(km),距终点还需行驶225 km,则有75t=900-200,解得t=$\frac{28}{3}$.
综上所述,两车恰好相距200 km的次数为5.
故选A.
5. 教材P125例3·变式 已知A,B两地相距300千米,甲车的速度为每小时75千米,乙车的速度为每小时45千米.
(1)若两车分别从A,B两地同时同向而行(甲车在乙车后面),经过多长时间甲车追上乙车?
(2)若两车同时从A,B两地相向而行,问:经过多长时间两车相距60千米?
答案:
(1)设经过x小时甲车追上乙车,
由题意,得75x-45x=300,解得x=10.
故经过10小时甲车追上乙车.
(2)设经过y小时两车相距60千米,
由题意,得75y+45y=300-60或75y+45y=300+60,
解得y=2或y=3.
故经过2小时或3小时两车相距60千米.
6. 分类讨论思想 (2025·南京联合体期末)如图是两张不同类型火车(“D×××次”表示动车,“G×××次”表示高铁)的车票:
|D×××次| |
|A地——→B地| |
|2023年9月29日|02车12号|
|¥360元|20:00|
|限乘当日当次车|A地售|

|G×××次| |
|A地——→B地| |
|2023年9月29日|03车13号|
|¥560元|21:00|
|限乘当日当次车|A地售|

(1)根据车票中的信息填空:该列动车和高铁是
同
(填“相”或“同”)向而行,该列动车比高铁发车
早
(填“早”或“晚”);
(2)已知该列动车和高铁的平均速度分别为200 km/h、300 km/h,两列火车的长度不计,高铁比动车早到1 h,求A,B两地之间的距离;
设A,B两地之间的距离为x km.根据题意,得$\frac{x}{200}-\frac{x}{300}=2$,解得x=1200.故A,B两地之间的距离为1200 km.
(3)在(2)的条件下,求高铁出发多少小时后两车相距150 km.
设高铁出发y小时后两车相距150 km,①当高铁还未追上动车时,200(y+1)-300y=150,解得y=$\frac{1}{2}$;②当高铁追上动车后,300y-200(y+1)=150,解得y=$\frac{7}{2}$;③当高铁到达B地后,200(y+1)=1200-150,解得y=$\frac{17}{4}$.故当高铁出发$\frac{1}{2}$h或$\frac{7}{2}$h或$\frac{17}{4}$h后两车相距150 km.
答案:
(1)同 早 [解析]由题图可知,该列动车和高铁是同向而行,该列动车比高铁发车早.
(2)设A,B两地之间的距离为x km.
根据题意,得$\frac{x}{200}-\frac{x}{300}=2$,
解得x=1200.
故A,B两地之间的距离为1200 km.
(3)设高铁出发y小时后两车相距150 km,
①当高铁还未追上动车时,200(y+1)-300y=150,解得y=$\frac{1}{2}$;
②当高铁追上动车后,300y-200(y+1)=150,解得y=$\frac{7}{2}$;
③当高铁到达B地后,200(y+1)=1200-150,解得y=$\frac{17}{4}$.
故当高铁出发$\frac{1}{2}$h或$\frac{7}{2}$h或$\frac{17}{4}$h后两车相距150 km.