1. 当$a= 2$,$b= -3$时,代数式$(a - b)^2 + 2ab$的值为(
A
).
A.13
B.27
C.-5
D.-7
答案:A
解析:
当$a = 2$,$b=-3$时,
$(a - b)^2 + 2ab=(2 - (-3))^2+2×2×(-3)$
$=(5)^2+(-12)$
$=25-12=13$
A
2. 中考新考法 满足条件的结论开放 (2025·无锡期末)若含$x$的代数式,满足当$x= 4$时,代数式的值为$-1$.请写出一个符合条件的代数式:
x-5
.
答案:x-5(答案不唯一)
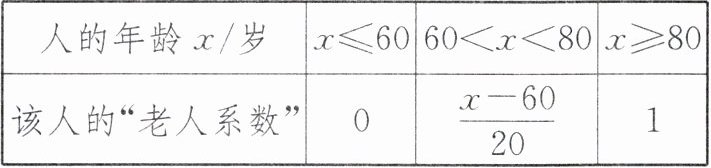
3. 日常生活中,“老人”是一个模糊概念.有人想用“老人系数”来表示一个人的老年化程度.他设想“老人系数”的计算方法如下表:
|人的年龄$x$/岁|$x\leqslant60$|$60<x<80$|$x\geqslant80$|
|该人的“老人系数”|0|$\frac{x - 60}{20}$|1|
按照这样的规定,一个 75 岁的人的“老人系数”为
0.75
.
答案:0.75
解析:
因为 $60 < 75 < 80$,所以“老人系数”为 $\frac{75 - 60}{20} = \frac{15}{20} = 0.75$。
0.75
|$n$|1|2|3|4|5|6|7|8|
|$5n + 10$|
15
|
20
|
25
|
30
|
35
|
40
|
45
|
50
|
|$n^2$|
1
|
4
|
9
|
16
|
25
|
36
|
49
|
64
|
(1)随着$n$的值逐渐变大,两个代数式的值如何变化?
随着n的值逐渐变大,两个代数式的值逐渐增大.
(2)估计一下,哪个代数式的值先超过 100?
代数式$n^{2}$的值先超过100.
答案:15 20 25 30 35 40 45 50
1 4 9 16 25 36 49 64
(1)随着n的值逐渐变大,两个代数式的值逐渐增大.
(2)代数式$n^{2}$的值先超过100.
5. 数学文化 多项式的记号表示法 (2024·广东广州荔湾区期末)历史上,数学家欧拉最先把关于$x的多项式用记号f(x)$来表示,把$x等于某数a时的多项式的值用f(a)$来表示,例如当$x= -1$时,多项式$f(x)= x^2 + 3x - 5的值记为f(-1)$,那么$f(-1)$等于(
A
).
A.-7
B.-9
C.-3
D.-1
答案:A
解析:
$f(-1)=(-1)^2 + 3×(-1) - 5=1 - 3 - 5=-7$
A
6. (2025·南通启东期中)下列代数式,满足表中条件的是(
C
).
|$x$|0|1|2|3|
|代数式的值|-3|-1|1|3|

A.$-x - 3$
B.$x^2 + 2x - 3$
C.$2x - 3$
D.$x^2 - 2x - 3$
答案:C [解析]
∵当x=0时,代数式的值为-3;当x=1时,代数式的值为-1;当x=2时,代数式的值为1,
∴只有2x-3满足此条件.故选C.
归纳总结 本题主要考查了代数式求值,正确利用代数式求值的方法是解题关键.
7. (南京鼓楼区金陵中学自主招生)$(x - 1)^5分解为a + bx + cx^2 + dx^3 + ex^4 + x^5$,则$a + c + e= $
-16
.
答案:-16
解析:
令$x=1$,则$(1 - 1)^5 = a + b×1 + c×1^2 + d×1^3 + e×1^4 + 1^5$,即$0 = a + b + c + d + e + 1$,得$a + b + c + d + e = -1$。
令$x=-1$,则$(-1 - 1)^5 = a + b×(-1) + c×(-1)^2 + d×(-1)^3 + e×(-1)^4 + (-1)^5$,即$-32 = a - b + c - d + e - 1$,得$a - b + c - d + e = -31$。
将上述两式相加:$(a + b + c + d + e) + (a - b + c - d + e) = -1 + (-31)$,即$2(a + c + e) = -32$,所以$a + c + e = -16$。
-16
8. 新情境 购买物品 (2025·无锡惠山区期末)某商店出售羽毛球拍和羽毛球,羽毛球拍每副定价1500元,羽毛球每桶定价100元,促销期间有两种付费方式:A. 买一副羽毛球拍赠送2桶羽毛球;B. 羽毛球拍和羽毛球都按定价的9折优惠.
(1)某训练队购买6副羽毛球拍和羽毛球$x(x>12)$桶,请你帮训练队计算两种付费金额(结果需化简).
(2)当$x= 35$时,通过计算说明哪种付费方式更划算?
答案:
(1)A方式:$1500×6 + 100(x - 12)=(100x + 7800)$元;
B方式:$1500×0.9×6 + 100×0.9x=(90x + 8100)$元.
(2)当x=35时,
$100x + 7800=3500 + 7800=11300,90x + 8100=3150 + 8100=11250$.
∵11300>11250,
∴B种付费方式更划算.
思路引导 本题考查列代数式及代数式求值,结合已知条件列得正确的代数式是解题的关键.