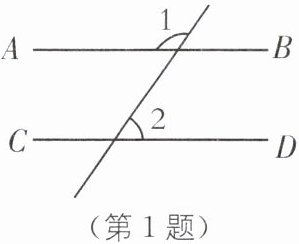
1. (2024·重庆中考)如图,$AB // CD$,若$\angle 1= 125^\circ$,则$\angle 2$的度数为(
C
).
A.$35^\circ$
B.$45^\circ$
C.$55^\circ$
D.$125^\circ$
答案:C
解析:
∵AB//CD,
∴∠1与∠2的邻补角相等(两直线平行,同位角相等),
∵∠1=125°,
∴∠2=180°-125°=55°。
C
2. (2024·南通海门区二模)若点C是线段AB的中点,且$BC= 3\ cm$,则AB的长是(
D
).
A.$1.5\ cm$
B.$3\ cm$
C.$4.5\ cm$
D.$6\ cm$
答案:D
解析:
因为点C是线段AB的中点,所以$AB=2BC$。已知$BC=3\ cm$,则$AB=2×3=6\ cm$。
D
3. (2024·兰州中考)如图,小明在地图上量得$\angle 1= \angle 2$,由此判断幸福大街与平安大街互相平行,他判断的依据是(
B
).

A.同位角相等,两直线平行
B.内错角相等,两直线平行
C.同旁内角互补,两直线平行
D.对顶角相等
答案:B
4. 如图,点O在直线AB上,$\angle AOC与\angle BOD$互余,$\angle AOD= 148^\circ$,则$\angle BOC$的度数为(
A
).

A.$122^\circ$
B.$132^\circ$
C.$128^\circ$
D.$138^\circ$
答案:A [解析]
∵点O在直线AB上,∠AOC与∠BOD互余,
∴∠AOC+∠BOD=90°,
∴∠COD=180°-(∠AOC+∠BOD)=180°-90°=90°.
∵∠AOD=148°,
∴∠BOD=180°-∠AOD=180°-148°=32°,
∴∠BOC=∠COD+∠BOD=90°+32°=122°.故选A
5. (2025·河南平顶山期末)将一副三角板的直角顶点重合按如图放置,$\angle C= 45^\circ$,$\angle D= 30^\circ$,小明得到下列结论:
①若$\angle 2= 30^\circ$,则$AC // DE$;
②$\angle BAE + \angle CAD= 180^\circ$;
③若$BC // AD$,则$\angle 2= 30^\circ$;
④若$\angle CAD= 150^\circ$,则$\angle 4= \angle C$.
其中正确的结论有(
C
).

A.1个
B.2个
C.3个
D.4个
答案:C
解析:
①
∵∠2=30°,∠CAB=90°,
∴∠1=60°.
∵∠D=30°,∠EAD=90°,
∴∠E=60°.
∴∠1=∠E,
∴AC//DE.正确.
②
∵∠BAE+∠CAD=∠BAE+∠1+∠2=∠CAB+∠EAD=90°+90°=180°.正确.
③
∵BC//AD,∠C=45°,
∴∠1=∠C=45°.
∵∠CAB=90°,
∴∠2=90°-45°=45°.错误.
④
∵∠CAD=150°,∠EAD=90°,
∴∠3=150°-90°=60°.
∵∠B=45°,
∴∠4=180°-∠B-∠3=75°.
∵∠C=45°,
∴∠4≠∠C.错误.
正确结论有①②,共2个.
B
6. 如图,直线a,b被直线c所截,能使$a // b$的条件是(
B
).

A.$\angle 1= \angle 2$
B.$\angle 1= \angle 3$
C.$\angle 1 + \angle 3= 180^\circ$
D.$\angle 2 + \angle 3= 180^\circ$
答案:B
7. (2024·南京鼓楼区期末)如图,$AC \perp BC$,$CD \perp AB$,垂足分别为C,D.下列说法正确的个数是(
C
).
①点C到线段AB的距离为线段CD的长度;
②$\angle ACD + \angle B= 90^\circ$;
③$\angle A= \angle BCD$;
④将三角形ABC绕线段BC所在直线旋转一周得到的几何体是圆锥.

A.1
B.2
C.3
D.4
答案:C [解析]①
∵点到直线的距离就是这个点到这条直线的垂线段的长度,CD⊥AB,
∴点C到线段AB的距离为线段CD的长度.故①说法正确;②
∵AC⊥BC,
∴∠ACB=∠ACD+∠BCD=90°.
∵CD⊥AB,
∴∠CDB=90°,
∴∠BCD+∠B=90°,
∴∠ACD=∠B.故②说法不正确;③
∵AC⊥BC,
∴∠ACB=∠ACD+∠BCD=90°.
∵CD⊥AB,
∴∠ADC=90°,
∴∠ACD+∠A=90°,
∴∠A=∠BCD.故③说法正确;④将三角形ABC绕线段BC所在直线旋转一周得到的几何体是圆锥.故④的说法正确综上所述,说法正确的是①③④,共3个.故选C
8. 早晨8:00以后,时钟的分针和时针第一次垂直的准确时间是(
C
).
A.8点$23\frac{1}{13}$分
B.8点25分
C.8点$27\frac{3}{11}$分
D.9点整
答案:C [解析]设t分后时钟的分针和时针第一次垂直,依题意,有6t - 0.5t = 360 - 120 - 90,解得t = 27$\frac{3}{11}$.故早晨8:00以后,时钟的分针和时针第一次垂直的准确时间是8点27$\frac{3}{11}$分.故选C
9. 如图,图中共有
1
条直线,
8
条射线,
6
条线段.
答案:1 8 6
10. (2024·南京玄武区期末)已知点A,B,C在同一条直线上,M,N分别是线段AB,BC的中点.若$AB= 6$,$BC= 2$,则$MN= $______.
答案:2或4 [解析]如图
(1),当点C在线段AB上时,
∵M,N分别为AB,BC的中点,
∴BM = $\frac{1}{2}$AB = 3,BN = $\frac{1}{2}$BC = 1,
∴MN = 3 - 1 = 2;

如图
(2),当点C在线段AB的延长线上时,同理可知BM = 3,BN = 1,
∴MN = 3 + 1 = 4.
∴MN = 2或4.

11. (2025·湖南邵阳邵东期末)如图,把原来弯曲的河道改直,A,B两地间的河道长度变短,这样做的道理是
两点之间,线段最短
.
答案:两点之间,线段最短