11. 在多边形边上或内部取一点与多边形各顶点的连线,将多边形分割成若干个小三角形.图(1)给出了四边形的具体分割方法,分别将四边形分割成了2个,3个,4个小三角形.
(1)请你根据上述方法将图(2)中的六边形进行分割,并写出得到的小三角形的个数;
(2)试把这一结论推广至n边形.
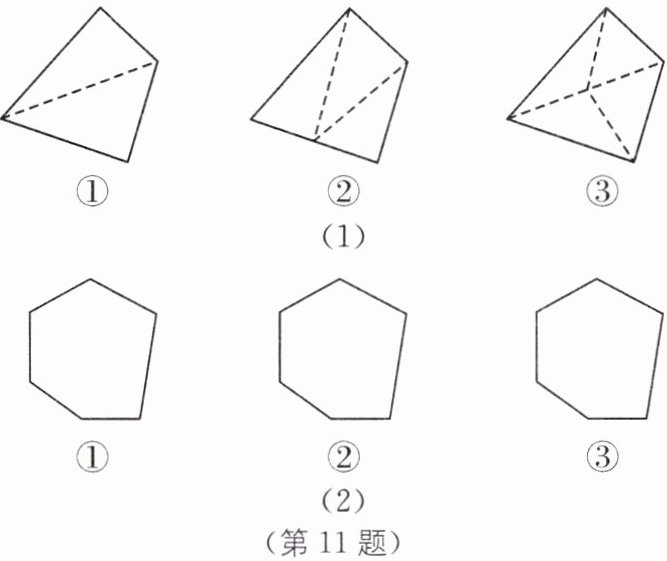
答案:(1)如图,得到的小三角形的个数分别为4,5,6.

(2)分割n边形时,若取多边形边上一点且该点为顶点时,该点与其他各顶点的连线将该多边形分割成(n-2)个三角形,若取多边形边上一点(非顶点),该点与各顶点的连线将该多边形分割成(n-1)个三角形;若取多边形内部一点,则该点与各顶点的连线,将该多边形分割成n个三角形.
12. 皮克模型 中考新考法 规律探究 探索题:
(1)在如图(1)的格点图中,各个多边形的内部都有而且只有1个格点.(相邻两格点的距离为1)
将各个多边形的面积与它四周各边上格点的个数填入下表,你能发现什么规律?
| 多边形序号 | ① | ② | ③ | ... |
| 多边形面积S |
2
|
3
|
2
| ... |
| 多边形边上格点的个数x |
4
|
6
|
4
| ... |
请写出S与x之间的关系式.
$S=\frac {1}{2}x$
(2)在如图(2)所示的格点图中,画出几个多边形,使其内部都有而且只有2个格点,再按第(1)题的做法,你发现此时各个多边形的面积与四周各边上的格点的个数之间又有什么样的关系呢?请写出S与x之间的关系式.
$S=\frac {1}{2}x+1$
(3)请你继续探索,当格点多边形内部有而且只有n个格点时,猜想S与x有怎么样的关系?
$S=\frac {1}{2}x+(n-1)$
答案:
(1)填表如下:
多边形序号 ① ② ③ …
多边形面积S 2 3 2 …
多边形边上格点的个数x 4 6 4 …
S与x之间的关系式为$S=\frac {1}{2}x.$
(2)图略(答案不唯一),$S=\frac {1}{2}x+1.$
(3)$S=\frac {1}{2}x+(n-1).$
素养考向 本题考查了作图——应用与设计作图,本题需要根据题中图表和自己所算出来的数据,总结规律,寻找规律需要仔细观察和大量验算,着重考查学生的抽象能力、模型观念和运算能力.