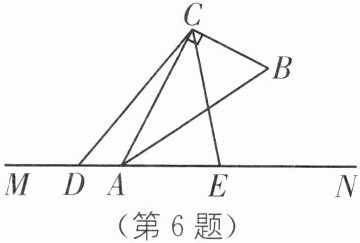
6. 分类讨论思想 中考新考法 满足结论的条件开放 (2024·广东佛山南海区期末)[综合探究]如图,在直角△ABC中,∠ACB= 90°,点A在直线MN上,点D,E在直线MN上运动(点D不与点A重合),且始终满足CE平分∠BCD.
(1)当点D在点A左侧时,请直接写出∠CAD与∠CAE之间的数量关系;
(2)若∠CAE= 60°,在点D,E运动过程中,当△CDE是直角三角形时,求∠DCE的度数;
(3)请你在以点C为顶点的角中任选一个(∠BCD,∠ACD,∠ACB除外),在点D,E运动的过程中,探究所选角与∠ACD的数量关系,并写出具体过程.
答案:(1)
∵点D,E在直线MN上运动,CE平分∠BCD,∠ACB=90°,
∴点E在点A的右侧
∵点D在点A左侧,
∴∠CAD+∠CAE=180°.
(2)
∵点D,E在直线MN上运动,CE平分∠BCD,∠ACB=90°,
∴点E在点A的右侧
∵△CDE是直角三角形,
∴∠CDE=90°或∠CED=90°,
①若∠CDE=90°,如图
(1),
则∠CAD=∠CAE=60°,∠CDA=∠CDE=90°,
∴∠ACD=180°−∠CDA−∠CAD=30°.
∵∠ACB=90°,
∴∠DCB=∠ACB−∠ACD=60°.
∵CE平分∠BCD,
∴∠DCE=∠ECB=$\frac{1}{2}$∠BCD=30°;

②若∠CED=90°,如图
(2).

∵∠CAE=60°,
∴∠ACE=180°−∠CEA−∠CAE=30°.
∵∠ACB=90°,
∴∠BCE=∠ACB−∠ACE=60°.
∵CE平分∠BCD,
∴∠DCE=∠ECB=60°.
综上所述,∠DCE=30°或∠DCE=60°.
(3)探究∠ACE与∠ACD的数量关系
∵点D,E在直线MN上运动,CE平分∠BCD,∠ACB=90°,
∴点E在点A的右侧
①点D在点A左侧时,如图
(3).

∵CE平分∠BCD,
∴∠ACD+∠ACE=∠BCE.
∵∠BCE=∠ACB−∠ACE=90°−∠ACE,
∴∠ACD+∠ACE=90°−∠ACE,
即∠ACD+2∠ACE=90°;
②点D在点A右侧时,如图
(4).
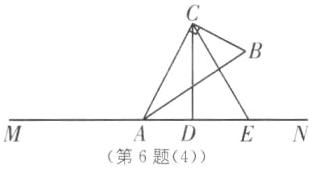
∵CE平分∠BCD,
∴∠DCE=∠ECB=$\frac{1}{2}$∠BCD.
∵∠ACE+∠ECB=∠ACB=90°,
∴∠ACD+∠BCD=∠ACD+2∠BCE=∠ACB=90°.则∠ACD+2(90°−∠ACE)=90°,
即2∠ACE−∠ACD=90°.
综上所述,∠ACE与∠ACD的数量关系为∠ACD+2∠ACE=90°或2∠ACE−∠ACD=90°.