1. (2025·宿迁宿豫区期末)下列选项中,过点A画BC的垂线AD,三角板摆放正确的是(
D
).
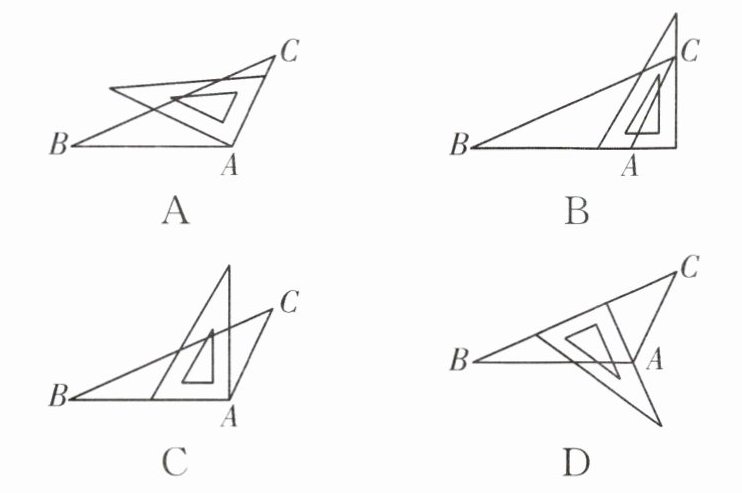
A.
B.
C.
D.
答案:D
2. (2025·重庆永川区期末)如图,OA⊥OD,∠AOC= 3∠COD,OC平分∠BOD,则∠AOB的度数为(
A
).

A.45°
B.46°
C.50°
D.60°
答案:A
解析:
∵OA⊥OD,
∴∠AOD=90°,
∵∠AOC=3∠COD,∠AOC+∠COD=∠AOD=90°,
∴3∠COD+∠COD=90°,
∴∠COD=22.5°,
∵OC平分∠BOD,
∴∠BOD=2∠COD=45°,
∴∠AOB=∠AOD-∠BOD=90°-45°=45°.
A
3. 如图,AO⊥OC,点B,O,D在同一条直线上,若∠1= 15°,则∠2的度数是
105°
.
答案:105°
解析:
∵AO⊥OC,
∴∠AOC=90°。
∵∠1=15°,
∴∠BOC=∠AOC - ∠1=90° - 15°=75°。
∵点B,O,D在同一条直线上,
∴∠2 + ∠BOC=180°,
∴∠2=180° - ∠BOC=180° - 75°=105°。
105°
4. 教材P175例2·变式 (2025·黑龙江齐齐哈尔期末)如图,点O是直线AB上一点,∠AOC= 40°,OD平分∠AOC,∠COE= 70°.
(1)请你说明DO⊥OE.
(2)OE平分∠BOC吗?为什么?

答案:
(1)
∵OD平分∠AOC,∠AOC=40°,
∴∠DOC=$\frac{1}{2}$∠AOC=20°.
∵∠COE=70°,
∴∠DOE=90°,
∴DO⊥OE.
(2)OE平分∠BOC.理由如下:
∵∠AOC+∠COE+∠BOE=180°,
且∠AOC=40°,∠COE=70°,
∴∠BOE=70°,
∴∠BOE=∠COE,
∴OE平分∠BOC.
5. (2025·山东济宁邹城期末)如图,直线AB,CD相交于点O,OF⊥CD,垂足为O,OE平分∠BOF,若∠DOE= 20°,则∠AOC的度数为(
C
).

A.20°
B.40°
C.50°
D.70°
答案:C [解析]
∵OF⊥CD,
∴∠DOF=90°.
∵∠DOE=20°,
∴∠EOF=90°−20°=70°.
∵OE平分∠BOF,
∴∠BOE=∠EOF=70°,
∴∠BOD=∠BOE−∠DOE=50°,
∴∠AOC=∠BOD=50°.故选C.
6. 如图,点O在直线AB上,OD⊥OE,垂足为O,OC是∠DOB的平分线,若∠AOD= 70°,则∠COE=
35
°.

答案:35 [解析]
∵∠AOD=70°,
∴∠BOD=180°−∠AOD=180°−70°=110°.
∵OC是∠DOB的平分线,
∴∠DOC=$\frac{1}{2}$∠BOD=$\frac{1}{2}$×110°=55°.
∵OD⊥OE,
∴∠DOE=90°
∴∠COE=∠DOE−∠DOC=90°−55°=35°.
7. (2024·南京玄武区期末)如图,直线AB,CD相交于点O,OE⊥CD,OF平分∠BOD,若∠AOE+∠BOF= 66°,则∠BOC= ______.

132°
答案:132° [解析]设∠AOE=α,∠BOF=β.
∵∠AOE+∠BOF=66°,
∴α+β=66°,
∴β=66°−α,
∵OF平分∠BOD,
∴∠DOF=∠BOF=β,
∴∠DOB=∠DOF+∠BOF=2β.
∵OE⊥CD,
∴∠EOD=90°.
∵∠AOE+∠EOD+∠DOB=180°,
∴α+90°+2β=180°,
∴α+2β=90°,
∴α+2(66°−α)=90°,解得α=42°,即∠AOE=42°,
∴∠AOD=∠AOE+∠EOD=42°+90°=132°,
∴∠BOC=∠AOD=132°.
8. 如图,直线AB,CD相交于点O,OE平分∠BOD,OF⊥OE,垂足为O,若∠AOC= 40°.
(1)求∠DOE的度数.(按要求填空)
解:∵直线AB,CD相交于点O(已知),
∴∠BOD= ∠AOC(
对顶角相等
).
∵∠AOC= 40°(已知),
∴(
∠BOD
)= 40°(等量代换).
∵OE平分∠BOD(已知),
∴∠DOE= $\frac{1}{2}$∠BOD(
角平分线的定义
).
∵(
∠BOD=40°
)(已证),
∴∠DOE= $\frac{1}{2}$∠BOD= (
20
)°(等式性质).
(2)OF平分∠BOC吗?为什么?
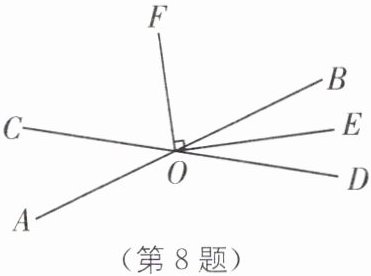
(2)OF平分∠BOC.理由如下:
∵∠COD=180°,∠EOF=90°,
∴∠COF+∠DOE=90°,
∴∠COF=70°.
∵∠BOF=90°−∠BOE=70°,
∴∠COF=∠BOF,即OF平分∠BOC.
答案:
(1)对顶角相等 ∠BOD 角平分线的定义
∠BOD=40° 20
(2)OF平分∠BOC.理由如下:
∵∠COD=180°,∠EOF=90°,
∴∠COF+∠DOE=90°,
∴∠COF=70°.
∵∠BOF=90°−∠BOE=70°,
∴∠COF=∠BOF,即OF平分∠BOC.