(1)如图(2),若点B′恰好落在OA′上,且∠AOC= 32°,则∠BOD=
58°
;
(2)如图(3),当点B′在∠COA′的内部时,连接OB′,若∠AOC= 44°,∠BOD= 61°,求∠A′OB′的度数为
30°
.
答案:
(1)58° [解析]由折叠知,∠AOC=∠A'OC,
∴∠AOA'=2∠AOC.
由折叠知,∠BOD=∠B'OD,
∴∠BOB'=2∠BOD.
∵点 B'落在 OA'上,
∴∠AOA'+∠BOB'=180°,
∴2∠AOC + 2∠BOD=180°,
∴∠AOC + ∠BOD=90°.
∵∠AOC=32°,
∴∠BOD=90° - 32°=58°.
(2)30° [解析]由折叠知,∠AOA'=2∠AOC,∠BOB'=2∠BOD.
∵∠AOC=44°,∠BOD=61°,
∴∠AOA'=2∠AOC=2×44°=88°,∠BOB'=2∠BOD=2×61°=122°,
∴∠A'OB'=∠AOA'+∠BOB' - 180°=88°+122° - 180°=30°,即∠A'OB'的度数为 30°.
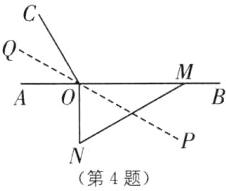
4.分类讨论思想(2025·河北衡水桃城区期中)如图,点O为直线AB上一点,过点O作射线OC,使∠BOC= 120°,将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB下方.将图中三角板绕点O逆时针旋转α(0°<α<360°),使得直线ON恰好平分∠AOC,则α= ______或______.
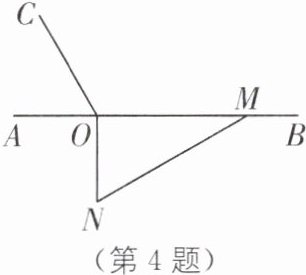
答案:60 240 [解析]设∠AOC 的平分线所在的直线为 PQ,如图所示.
∵∠BOC=120°,
∴∠AOC=180° - 120°=60°,
∴∠AOQ=∠COQ=∠BOP=30°,
∴∠NOP=90° - 30°=60°.
当 ON 与射线 OP 重合时,此时旋转角为 60°;
当 ON 与射线 OQ 重合时,此时旋转角为 90°+120°+30°=240°.
关键提醒 本题考查角平分线的意义、旋转的意义,明确角平分线和旋转的意义是解决问题的关键,分类讨论解答是此类题目的共同特点.
变式4.1 (2025·辽宁抚顺新宾期末)综合与实践已知,O为直线AB上的一点,过点O作射线OC,使∠BOC= 65°,将一直角三角板的直角顶点放在点O处.
(1)如图(1),将三角板MON的一边ON与射线OB重合,此时∠MOC= ______
25°
;
(2)如图(2),将三角板MON绕点O逆时针旋转一定角度,使得OC是∠MOB的平分线,求∠CON的度数;
依题意,得∠BOC=65°,∠MON=90°.∵OC 是∠MOB 的平分线,∴∠MOC=∠BOC=65°,∴∠CON=∠MON - ∠MOC=90° - 65°=25°.
(3)如图(3),将三角板MON继续绕点O逆时针旋转至∠AOC内部,使得$∠NOC= \frac{1}{4}∠AOM.$求∠MOC的度数.
设∠NOC=α.∵∠NOC=$\frac{1}{4}$∠AOM,∴∠AOM=4∠NOC=4α.∵∠BOC=65°,∠AOC 和∠BOC 互补,∴∠AOC=180° - ∠BOC=180° - 65°=115°.又∠AOC=∠AOM + ∠MON + ∠NOC,∠MON=90°,∴4α + 90°+α=115°,解得 α=5°,∴∠NOC=α=5°,∴∠MOC=∠MON + ∠NOC=90°+5°=95°.
答案:
(1)25° [解析]依题意,得∠BOC=65°,∠MOB=90°,
∴∠MOC 和∠BOC 互余,∠MOC=∠MOB - ∠BOC=90° - 65°=25°.
(2)依题意,得∠BOC=65°,∠MON=90°.
∵OC 是∠MOB 的平分线,
∴∠MOC=∠BOC=65°,
∴∠CON=∠MON - ∠MOC=90° - 65°=25°.
(3)设∠NOC=α.
∵∠NOC=$\frac{1}{4}$∠AOM,
∴∠AOM=4∠NOC=4α.
∵∠BOC=65°,∠AOC 和∠BOC 互补,
∴∠AOC=180° - ∠BOC=180° - 65°=115°.
又∠AOC=∠AOM + ∠MON + ∠NOC,∠MON=90°,
∴4α + 90°+α=115°,解得 α=5°,
∴∠NOC=α=5°,
∴∠MOC=∠MON + ∠NOC=90°+5°=95°.
关键提醒 本题主要考查了角平分线的定义,互为余角和补角的概念,熟练掌握角平分线的定义,理解互为余角和补角的概念是解决问题的关键.