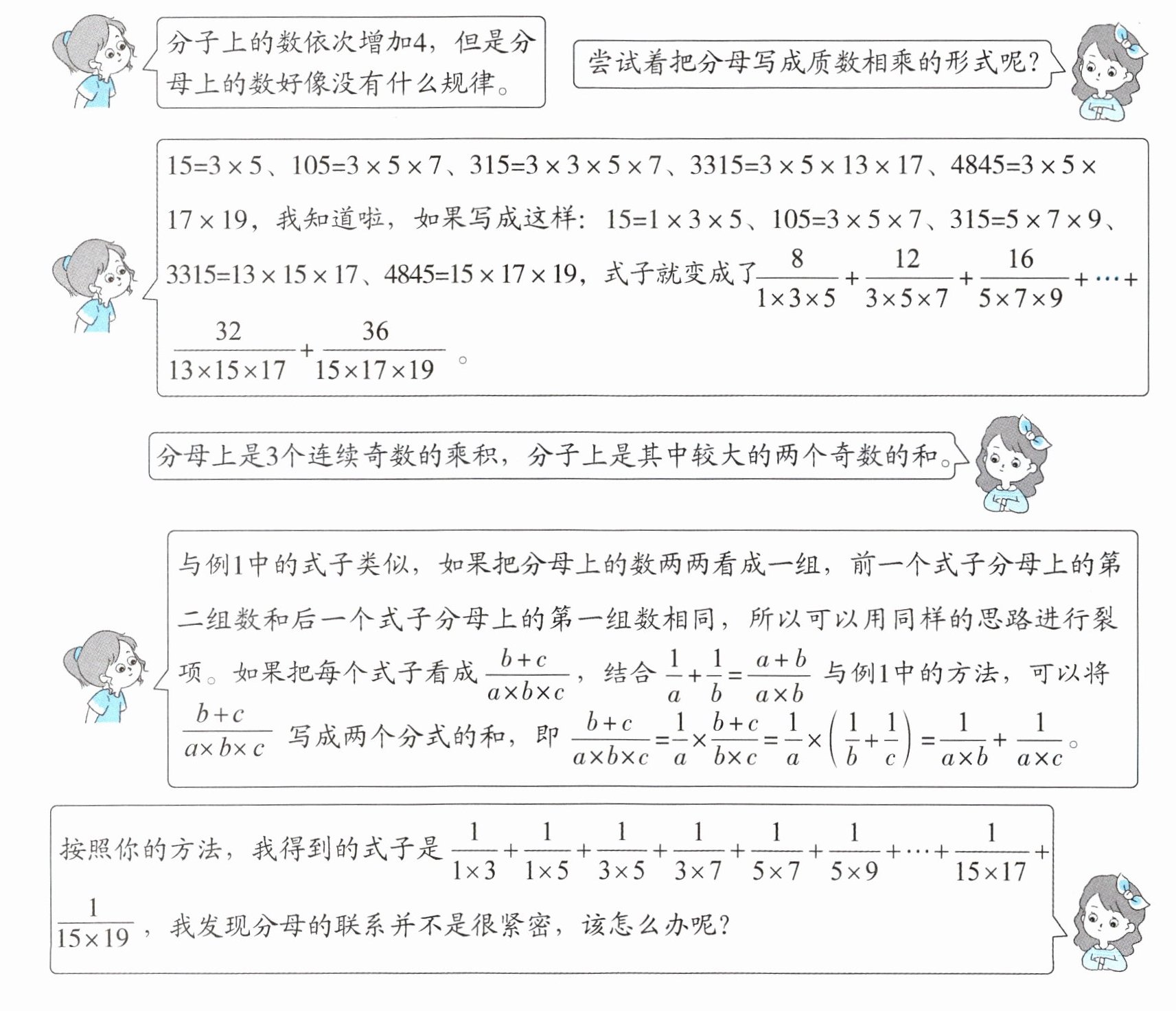
2025年学霸甘肃少年儿童出版社六年级数学上册苏教版第106页解析答案

例2 计算：$\frac {8}{15}+\frac {12}{105}+\frac {16}{315}+... +\frac {32}{3315}+\frac {36}{4845}$。
我的思考

我的尝试

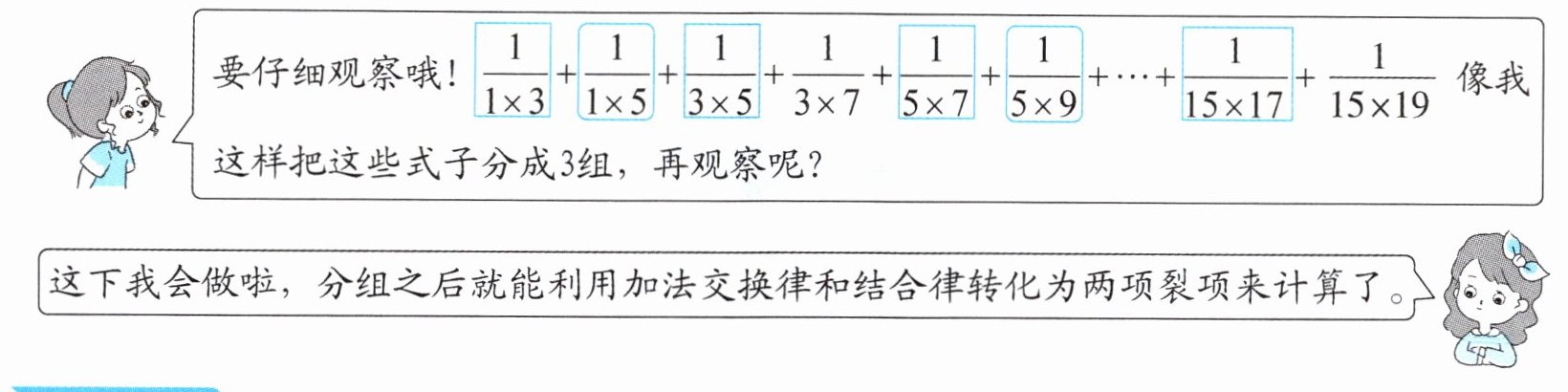
$\frac {8}{15}+\frac {12}{105}+\frac {16}{315}+... +\frac {32}{3315}+\frac {36}{4845}=\frac {8}{1×3×5}+\frac {12}{3×5×7}+\frac {16}{5×7×9}+... +\frac {36}{15×17×19}=\frac {3+5}{1×3×5}+\frac {5+7}{3×5×7}+\frac {7+9}{5×7×9}+... +\frac {17+19}{15×17×19}=\frac {1}{1×3}+\frac {1}{1×5}+\frac {1}{3×5}+\frac {1}{3×7}+\frac {1}{5×7}+\frac {1}{5×9}+... +\frac {1}{15×17}+\frac {1}{15×19}=(\frac {1}{1×3}+... +)+(\frac {1}{1×5}+... +)+(\frac {1}{3×7}+... +)====$
我的总结
在计算表面上没有规律的多个分数的和时,可以先将各个分数的分母写成质数相乘的形式(分解质因数),观察各个分母之间有无明显的倍数关系,或者找出各个分母的因数之间的排列规律,进而寻求简化运算的方法。
在三项裂项的分数巧算中,不仅要观察每个分数分子和分母上的数的关系,还要观察前后两个或三个分数分母之间的关系,灵活运算,将算式转化为一个或多个两项裂项的式子来计算。
在用裂项法计算多个分数的和时,常用的运算只有两个非零自然数的倒数之和、倒数之差,以及两个非零自然数与同一个非零自然数乘积的倒数之和、倒数之差,对应的分式公式只需能推导出即可。

答案：@@原式$=\frac {8}{1×3×5}+\frac {12}{3×5×7}+\frac {16}{5×7×9}+... +\frac {32}{13×15×17}+\frac {36}{15×17×19}$$=\left(\frac{1}{1× 3}+\frac{1}{1× 5}\right)+\left(\frac{1}{3× 5}+\frac{1}{3× 7}\right)+\left(\frac{1}{5× 7}+\frac{1}{5× 9}\right)+\cdots +\left(\frac{1}{13× 15}+\frac{1}{13× 17}\right)+\left(\frac{1}{15× 17}+\frac{1}{15× 19}\right)$$=\left(\frac{1}{1× 3}+\frac{1}{3× 5}+\frac{1}{5× 7}+\cdots +\frac{1}{15× 17}\right)+\left(\frac{1}{1× 5}+\frac{1}{3× 7}+\frac{1}{5× 9}+\cdots +\frac{1}{15× 19}\right)$第一组：$\frac{1}{1× 3}+\frac{1}{3× 5}+\frac{1}{5× 7}+\cdots +\frac{1}{15× 17}$$=\frac{1}{2}× \left(1 - \frac{1}{3}\right)+\frac{1}{2}× \left(\frac{1}{3}-\frac{1}{5}\right)+\frac{1}{2}× \left(\frac{1}{5}-\frac{1}{7}\right)+\cdots +\frac{1}{2}× \left(\frac{1}{15}-\frac{1}{17}\right)$$=\frac{1}{2}× \left(1 - \frac{1}{3}+\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+\cdots +\frac{1}{15}-\frac{1}{17}\right)$$=\frac{1}{2}× \left(1 - \frac{1}{17}\right)$$=\frac{1}{2}× \frac{16}{17}$$=\frac{8}{17}$第二组：$\frac{1}{1× 5}+\frac{1}{3× 7}+\frac{1}{5× 9}+\cdots +\frac{1}{15× 19}$$=\frac{1}{4}× \left(1 - \frac{1}{5}\right)+\frac{1}{4}× \left(\frac{1}{3}-\frac{1}{7}\right)+\frac{1}{4}× \left(\frac{1}{5}-\frac{1}{9}\right)+\cdots +\frac{1}{4}× \left(\frac{1}{15}-\frac{1}{19}\right)$$=\frac{1}{4}× \left(1+\frac{1}{3}-\frac{1}{17}-\frac{1}{19}\right)$$=\frac{1}{4}× \left(\frac{4}{3}-\frac{36}{323}\right)$$=\frac{1}{4}× \frac{1292 - 108}{969}$$=\frac{1}{4}× \frac{1184}{969}$$=\frac{296}{969}$原式$=\frac{8}{17}+\frac{296}{969}$$=\frac{456}{969}+\frac{296}{969}$$=\frac{752}{969}$$\frac{752}{969}$
@@$(\frac{1}{1×3}+\frac{1}{3×5}+\cdots+\frac{1}{15×17})+(\frac{1}{1×5}+\frac{1}{5×9}+\cdots+\frac{1}{13×17})+(\frac{1}{3×7}+\frac{1}{7×11}+\cdots+\frac{1}{15×19})=\frac{1}{2}×(\frac{2}{1×3}+\frac{2}{3×5}+\cdots+\frac{2}{15×17})+\frac{1}{4}×(\frac{4}{1×5}+\frac{4}{5×9}+\cdots+\frac{4}{13×17})+\frac{1}{4}×(\frac{4}{3×7}+\frac{4}{7×11}+\cdots+\frac{4}{15×19})=\frac{1}{2}×(1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+\cdots+\frac{1}{15}-\frac{1}{17})+\frac{1}{4}×(1-\frac{1}{5}+\frac{1}{5}-\frac{1}{9}+\cdots+\frac{1}{13}-\frac{1}{17})+\frac{1}{4}×(\frac{1}{3}-\frac{1}{7}+\frac{1}{7}-\frac{1}{11}+\cdots+\frac{1}{15}-\frac{1}{19})=\frac{1}{2}×\frac{16}{17}+\frac{1}{4}×\frac{16}{17}+\frac{1}{4}×\frac{16}{57}=\frac{752}{969}$