7. 同学们在探究梯形面积公式时,有以下几种方法:
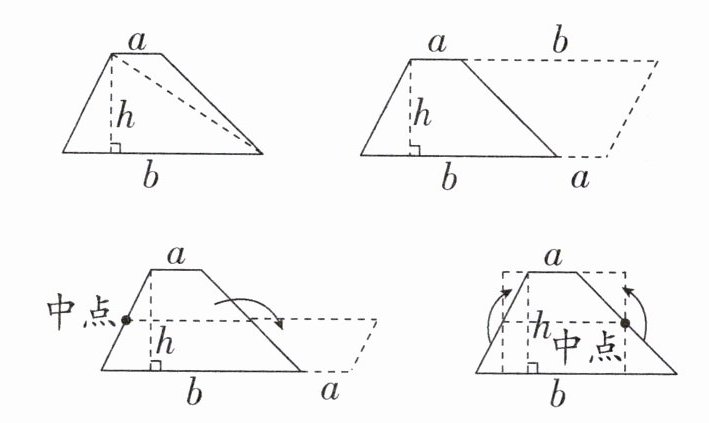
这四种转化方法对应的算式分别是(
C
)、(
A
)、(
B
)和(
D
)。
A.$(a + b)×h÷2$
B.$(a + b)×(h÷2)$
C.$ah÷2 + bh÷2$
D.$(a + b)÷2×h$
答案:C A B D
8. 数形结合

(1)根据梯形的面积公式计算上面两堆木头分别有多少根?
第一堆:
(1+6)×6÷2=21(根)
第二堆:
(2+6)×5÷2=20(根)
(2)如果最上层摆放了5根,最下层摆放了18根,这堆木头一共有(
161
)根。
(3)借助上面的方法可知:$1 + 2 + 3 + … + 99 + 100 = $(
1
+
100
)×
100
÷2 =
5050
。
答案:
(1)(1+6)×6÷2=21(根)
(2+6)×5÷2=20(根)
(2)161
(3)1 100 1005050
9. 下面三块菜地均靠着一面墙,且都是用40米长的篱笆围起来的,几号菜地的面积最小? 是多少平方米?

答案:①:10×(40 - 10)÷2=150(平方米)
②:(40 - 10)×8÷2=120(平方米)
③:(40 - 10)×10÷2=150(平方米)
120<150 ②号菜地的面积最小,是120平方米。
10.(1)如图,涂色部分的面积比空白部分的面积少24平方厘米,梯形的面积是(
120
)平方厘米。
(2)如图,涂色部分的面积为36平方厘米,$AB = $(
3
)厘米。
(3)如图,四边形ABCD是一个梯形,E是AD的中点,CE把梯形分成一个三角形(甲)和一个四边形(乙),甲的面积是3,乙的面积是5,下底CD的长度是上底AB长度的(
3
)倍。
答案:
(1)120
(2)3
(3)3
11. 如图,在直角梯形ABCD中,$AB = 30$分米,$∠1 = ∠2 = 45^{\circ}$,求梯形ABCD的面积。

答案:30×30÷2=450(平方分米) 提示:根据“∠1 = ∠2 = 45°”可知,三角形BCE是等腰直角三角形,则BC = BE。由于∠AED、∠DEC(直角)、∠2组成了一个平角,则∠AED = 180° - 90° - 45° = 45°。在直角三角形ADE中,∠ADE = 90° - 45° = 45°,则∠AED = ∠ADE,直角三角形ADE也是一个等腰直角三角形,则AD = AE。由此可得BC + AD = BE + AE = AB = 30分米,也就是梯形ABCD的上、下底的和是30分米,所以它的面积是30×30÷2 = 450(平方分米)。
解析:
因为∠1=∠2=45°,∠CBE=90°,所以△BCE是等腰直角三角形,故BC=BE。
因为∠DEC=90°,∠2=45°,∠AED+∠DEC+∠2=180°,所以∠AED=180°-90°-45°=45°。
因为∠DAE=90°,∠AED=45°,所以△ADE是等腰直角三角形,故AD=AE。
所以AD+BC=AE+BE=AB=30分米。
梯形ABCD的高等于AB的长度,即30分米。
梯形面积公式为$\frac{(上底 + 下底)×高}{2}$,所以面积为$\frac{30×30}{2}=450$平方分米。
答:梯形ABCD的面积是450平方分米。
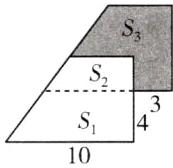
12. 如图,两个相同的直角梯形重叠在一起,你能求出涂色部分的面积吗? (单位:厘米)

答案:(10 - 3 + 10)×4÷2=34(平方厘米) 提示:如图,S₁+S₂ = S₃+S₂,可知S₁ = S₃,而S₁ = [(10 - 3)+10]×4÷2 = 34(平方厘米),所以S₃ = 34平方厘米。
13. 如图,$BO = 2DO$,涂色部分的面积是4平方厘米。那么梯形ABCD的面积是多少平方厘米?

答案:4÷2 = 2(平方厘米) 4×3 = 12(平方厘米) 12 + 4 + 2 = 18(平方厘米) 提示:如图,因为BO = 2DO,取BO的中点E,连接AE,则DO = OE = BE,三角形AOD、三角形AOE和三角形ABE等底等高,所以这三个三角形的面积相等。又因为三角形ABD和三角形ABC同底等高,这两个三角形公共部分是三角形ABO,所以三角形ADO和三角形BCO的面积相等,三角形AOD、三角形AOE和三角形ABE的面积都是4平方厘米。因为BO = 2DO,所以三角形COD的面积是三角形COB面积的一半,即三角形COD的面积 = 4÷2 = 2(平方厘米)。所以梯形的面积 = 4×3 + 4 + 2 = 18(平方厘米)。
