2. 下面为五(1)班男、女生 1 分钟跳绳测试等级情况的统计图:
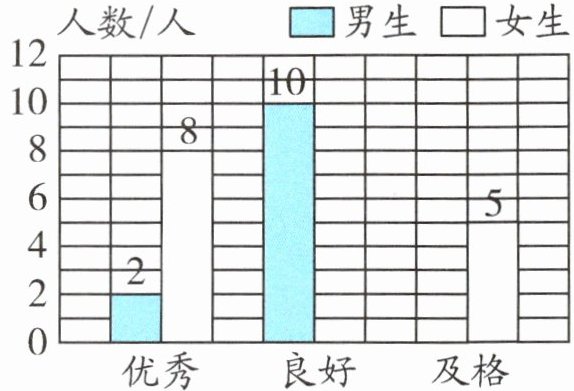
(1) 女生共有 22 人,及格等级的总人数是 16 人。请将统计图补充完整。
(2) 五(1)班一共有( )名学生,( )等级的男、女生人数相差最小。
(3) 如果将男生跳绳成绩从高到低排序,乐乐排在第 12 名,那么他跳绳成绩的等级是( )。
答案:
(2)45 良好
(3)良好
3. 小聪用一根绳子测一口枯井的深度。若将绳子的一端垂到井底,则另一端超过井口 8.4 米;若将绳子对折三次,一端垂到井底,则另一端正好与井口齐平。该井的深度是多少米?绳子的全长是多少米?
答案:井深:8.4÷(8-1)=1.2(米) 绳全长:1.2+8.4=9.6(米)
解析:
井深:$8.4÷(8 - 1)=1.2$(米)
绳全长:$1.2 + 8.4=9.6$(米)
4. 如图,四边形 ABCD 是平行四边形,BC 长 16 厘米,CE 长 10 厘米。已知平行四边形 ABCD 的面积比三角形 BCE 的面积大 32 平方厘米,求线段 EF 的长度。

答案:由题意可知,FC的长度是平行四边形ABCD的高,由题意得平行四边形ABCD的面积=三角形BCE的面积+32=16×10÷2+32=112(平方厘米),FC=112÷16=7(厘米),EF=EC-FC=10-7=3(厘米)。提示:根据题意,由平行四边形ABCD的面积比三角形BCE的面积大32平方厘米可知,平行四边形ABCD的面积=三角形BCE的面积+32平方厘米,已知三角形BCE的底是16厘米,高是10厘米,利用三角形面积公式求出其面积,再用其面积加上32平方厘米求出平行四边形ABCD的面积,已知平行四边形ABCD的底为16厘米,代入平行四边形面积计算公式即可求出高为7厘米,进而求出EF的长度。
解析:
三角形BCE的面积:$S_{\triangle BCE}=\frac{1}{2}× BC× CE=\frac{1}{2}×16×10=80$(平方厘米)
平行四边形ABCD的面积:$S_{□ ABCD}=S_{\triangle BCE}+32=80+32=112$(平方厘米)
平行四边形ABCD的高FC:$FC=S_{□ ABCD}÷ BC=112÷16=7$(厘米)
EF的长度:$EF=EC-FC=10-7=3$(厘米)
答:线段EF的长度为3厘米。
(1) 秦老师开小轿车到城东附近的朋友家做客,该区域属于一类地区。她停入车位时是 15:00,当天 18:30 开车离开车位。秦老师要缴(
47.5
)元停车费。
(2) 张叔叔开小轿车去通州办事,该区域位于三类地区,他停入车位时是上午 10:40,开车离开车位时缴了 18.5 元停车费(停车时间是 15 分钟的整数倍)。张叔叔几时开车离开了车位?
张叔叔17:10(下午5时10分)离开了车位
答案:
(1)47.5
(2)(18.5-0.5×4)÷(0.75×4)=5.5(小时)5.5+1=6.5(小时) 张叔叔17:10(下午5时10分)离开了车位提示:根据题意,三类地区小型车的收费标准为首小时内0.5元/15分,首小时后0.75元/15分,首小时内的收费为0.5×4=2(元),用超出部分的收费除以超出部分的收费标准得到张叔叔多停的时间,由此计算出张叔叔总共停车的时间,加上开始停车的时刻,得到他离开车位的时刻。
强基直通车 几位裁判员为一位体操运动员评分,去掉一个最高分后,平均成绩为 8.82 分。如果记入最高分,平均成绩为 9.04 分。已知这位运动员的最高分是 9.70 分,问:共有几位裁判员?
答案:(9.70-9.04)÷(9.04-8.82)+1=4(位)提示:9.70分比9.04分多0.66分,这0.66分必须填补到其他几位裁判员成绩中,使平均成绩由8.82分变为9.04分,平均每个裁判员的评分填补9.04-8.82=0.22(分),0.66里面有3个0.22,所以其他裁判员有3位,连评分最高的在内一共有3+1=4(位)裁判员。
解析:
最高分比记入最高分后的平均分高:$9.70 - 9.04 = 0.66$(分)
记入最高分后的平均分比去掉最高分后的平均分高:$9.04 - 8.82 = 0.22$(分)
其他裁判员人数:$0.66 ÷ 0.22 = 3$(位)
裁判员总人数:$3 + 1 = 4$(位)
答:共有4位裁判员。