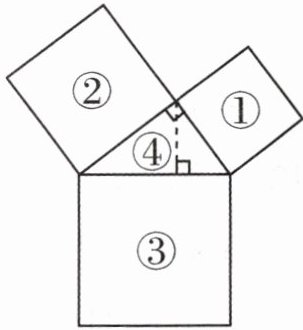
2. 如图是王轩家的四块菜地,①②③号菜地都是正方形,其中①号菜地和②号菜地的面积分别是9平方米和16平方米。④号菜地斜边上的高为2.4米。求③号菜地的面积。
答案:因为3×3=9(平方米),4×4=16(平方米),所以①号菜地和②号菜地的边长分别是3米和4米。④号菜地面积:3×4÷2=6(平方米) ③号菜地边长:6×2÷2.4=5(米) ③号菜地面积:5×5=25(平方米)
解析:
因为$3×3 = 9$(平方米),$4×4 = 16$(平方米),所以①号菜地和②号菜地的边长分别是$3$米和$4$米。
④号菜地面积:$\frac{1}{2}×3×4=6$(平方米)
③号菜地边长:$6×2÷2.4 = 5$(米)
③号菜地面积:$5×5 = 25$(平方米)
3. 在游乐园门口有一张价目表。骑木马:每10分钟2元;电动火车:每10分钟5元;碰碰车:每10分钟10元。小明想在游乐园玩30分钟,他可能花的钱有多少种情况?
答案:10种 ①2×3=6(元);②5×3=15(元);③10×3=30(元);④2×2+5=9(元);⑤2+5×2=12(元);⑥2×2+10=14(元);⑦2+10×2=22(元);⑧5×2+10=20(元);⑨5+10×2=25(元);⑩2+5+10=17(元)。
解析:
10种
①$2×3=6$(元)
②$5×3=15$(元)
③$10×3=30$(元)
④$2×2 + 5=9$(元)
⑤$2 + 5×2=12$(元)
⑥$2×2 + 10=14$(元)
⑦$2 + 10×2=22$(元)
⑧$5×2 + 10=20$(元)
⑨$5 + 10×2=25$(元)
⑩$2 + 5 + 10=17$(元)
4. 5个评委给歌手打分,按照规定,要去掉一个最高分和一个最低分,再算出平均分,这个歌手最后得分是9.4分,评委4打了多少分?
9.4×3-9.25-9.55=9.4(分)
答案:9.4×3-9.25-9.55=9.4(分)
5. 甲、乙两辆汽车同时从A地出发,将一批货物送到距离270千米的B地。甲车比乙车早到1.5小时,当甲车到达时,乙车距离B地还有90千米。甲车从A地到B地用了多少小时?
答案:270÷(90÷1.5)-1.5=3(小时)
解析:
乙车速度:$90÷1.5 = 60$(千米/小时)
乙车行驶全程时间:$270÷60 = 4.5$(小时)
甲车行驶全程时间:$4.5 - 1.5 = 3$(小时)
答:甲车从A地到B地用了3小时。
6. 数学考试后,第一次算出班级第一组同学的平均分是92.4分,复查时发现将其中一个98分误算成89分了。经重新计算,这个组的平均分为93分。这个组共有多少人参加了考试? (第一组同学全部参加了考试)
答案:(98-89)÷(93-92.4)=15(人)
7. 某市的出租车收费标准:起步价为3千米9元,白天超出部分每千米收2.4元;晚间(23:00到次日5:00)超出部分每千米收2.7元。(不足1千米按1千米计算)
(1)若用x(x为整数,且$x>3$)表示白天打车行驶的千米数,用y表示付的钱数,则它们之间的关系可以用式子表示为$y=$
9+2.4(x-3)
。
(2)王叔叔凌晨1:00从家赶到医院,乘出租车付了22.5元。他家到医院最多有多少千米?
3+(22.5-9)÷2.7=8(千米)
答案:
(1)9+2.4(x-3) 提示:如图,一共行驶x千米,前3千米共收费9元,那么剩下的(x-3)千米,每千米收费2.4元,所以付的钱数y=9+2.4(x-3)。
(2)3+(22.5-9)÷2.7=8(千米) 提示:起步价为3千米9元,剩下的22.5-9=13.5(元)最多还能行驶13.5÷2.7=5(千米),所以从王叔叔家到医院最多有3+5=8(千米)。
强基直通车
如图,四边形ABCD是一个长方形,点E在CD的延长线上,已知$AB= 5$厘米,$BC= 12$厘米,且三角形AFE的面积等于20平方厘米,那么三角形CFE的面积等于多少?

答案:S_{三角形ABE}=5×12÷2=30(平方厘米) S_{三角形ABF}=30-20=10(平方厘米) AF=10×2÷5=4(厘米) ED=20×2÷4=10(厘米) S_{三角形CFE}=(5+10)×(12-4)÷2=60(平方厘米) 提示:已知AB=5厘米,BC=12厘米,那么三角形ABE的面积就是5×12÷2=30(平方厘米)。又因为三角形AFE的面积是20平方厘米,因此三角形ABF的面积是30-20=10(平方厘米),AF的长度为10×2÷5=4(厘米)。在三角形AFE中,ED是AF边上对应的高,所以ED的长度为20×2÷4=10(厘米)。在三角形CEF中,底边CE=5+10=15(厘米),高FD=12-4=8(厘米),因此S_{三角形CFE}=(5+10)×(12-4)÷2=60(平方厘米)。
解析:
$S_{\triangle ABE}=5×12÷2=30$(平方厘米)
$S_{\triangle ABF}=30 - 20=10$(平方厘米)
$AF=10×2÷5=4$(厘米)
$ED=20×2÷4=10$(厘米)
$S_{\triangle CFE}=(5 + 10)×(12 - 4)÷2=60$(平方厘米)
答:三角形$CFE$的面积等于$60$平方厘米。