9. 将一张底是12厘米、高是8厘米的平行四边形纸片按如图所示的方法折叠,则涂色部分的面积是多少平方厘米?
]
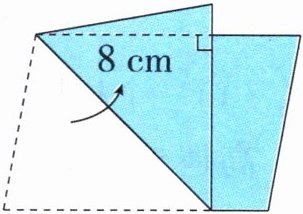
答案:9.12×8-8×8÷2=64(平方厘米)
10. 在如图的长方形ABCD中,三角形ADE、四边形DEBF和三角形CDF的面积都相等,求三角形DEF的面积。
]

答案:10.12×9÷3=36(平方厘米) BE的长是9-36×2÷12=3(厘米) BF的长是12-36×2÷9=4(厘米) 三角形EBF的面积是3×4÷2=6(平方厘米) 三角形DEF的面积是36-6=30(平方厘米) 提示:由题意可知,组成长方形的三个图形面积相等,则每个图形的面积都是12×9÷3=36(平方厘米),再求出三角形DEF的面积即可。
解析:
长方形ABCD的面积为$12×9 = 108$平方厘米。
因为三角形ADE、四边形DEBF和三角形CDF的面积都相等,所以每个图形的面积为$108÷3 = 36$平方厘米。
在三角形ADE中,$AD = 12$厘米,设$AE = x$厘米,根据三角形面积公式$\frac{1}{2}× AD× AE = 36$,可得$\frac{1}{2}×12× x = 36$,解得$x = 6$厘米,所以$BE = AB - AE = 9 - 6 = 3$厘米。
在三角形CDF中,$CD = 9$厘米,设$CF = y$厘米,根据三角形面积公式$\frac{1}{2}× CD× CF = 36$,可得$\frac{1}{2}×9× y = 36$,解得$y = 8$厘米,所以$BF = BC - CF = 12 - 8 = 4$厘米。
三角形EBF的面积为$\frac{1}{2}× BE× BF = \frac{1}{2}×3×4 = 6$平方厘米。
四边形DEBF的面积为36平方厘米,所以三角形DEF的面积为四边形DEBF的面积减去三角形EBF的面积,即$36 - 6 = 30$平方厘米。
答:三角形DEF的面积是30平方厘米。
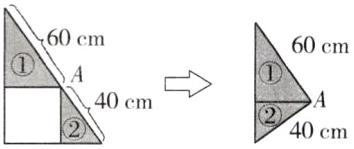
11. 转化思想 如图,大直角三角形中的空白部分是一个正方形,求涂色部分的面积。
]

答案:11.60×40÷2=1200(平方厘米) 提示:如图,将三角形②绕点A顺时针旋转90°,①和②就拼成了一个直角三角形,两条直角边分别为60厘米和40厘米。
12. 如图,P是平行四边形ABCD外的一点,三角形PAD的面积是20平方分米,三角形PBC的面积是45平方分米。求平行四边形ABCD的面积。
]

答案:12.45×2-20×2=50(平方分米) 提示:如图,过点P作AD的平行线,并分别与BA、CD的延长线相交于F、E两点,这样就得到了一个大平行四边形BCEF。观察可知,三角形PBC与平行四边形BCEF同底等高,则平行四边形BCEF的面积为45×2=90(平方分米);同理,平行四边形ADEF的面积为20×2=40(平方分米)。要求平行四边形ABCD的面积,只需用平行四边形BCEF的面积减去平行四边形ADEF的面积。
