5. 如图,一个梯形的上底延长 9 厘米后,变成了一个平行四边形,面积增加了 54 平方厘米,原来梯形的面积是多少?
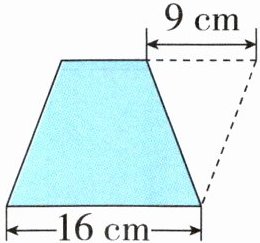
答案:5.高:54×2÷9=12(厘米) 16×12 - 54=138(平方厘米)
解析:
高:$54×2÷9 = 12$(厘米)
原来梯形的面积:$16×12 - 54=138$(平方厘米)
6. 林浅把一个长 30 厘米、宽 12 厘米的长方形框架拉成一个高 15 厘米的平行四边形,这个平行四边形的面积是多少? 如果拉成的平行四边形比原来长方形面积减少 60 平方厘米,那么拉成的平行四边形的高可能是多少厘米?
答案:6.12×15=180(平方厘米) 30×12 - 60=300(平方厘米) 300=30×10=12×25 所以拉成的平行四边形的高可能是10厘米,也可能是25厘米。
解析:
12×15=180(平方厘米)
30×12 - 60=300(平方厘米)
300÷30=10(厘米)
300÷12=25(厘米)
答:这个平行四边形的面积是180平方厘米;拉成的平行四边形的高可能是10厘米或25厘米。
7. 如图,孙大伯家用 70 米长的篱笆靠墙围了一个花圃。如果他从这个花圃中分出一块最大的三角形地种月季,面积是 360 平方米,这个梯形花圃较短的一条底边长多少米?

答案:7.360×2÷30=24(米) 70 - 30 - 24=16(米)
解析:
360×2÷30=24(米)
70 - 30 - 24=16(米)
答:这个梯形花圃较短的一条底边长16米。
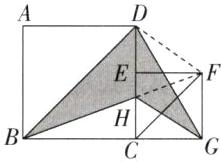
8. 如图,两个正方形并排放在一起,正方形 $ ABCD $的边长是 8 厘米,$ BD $与 $ FC $平行,求涂色部分的面积。

答案:8.8×8÷2=32(平方厘米)
提示:如图,连接FD,三角形DHG的面积等于三角形DHF的面积,因为BD与FC平行,所以涂色部分的面积=三角形DBF的面积=三角形DBC 的面积=8×8÷2=32(平方厘米)。
9. 如图,三角形 $ ABC $的底边 $ BC $和对应的高都是 4 厘米,点 $ A $和点 $ C $同时以每秒 2 厘米的速度向右平移,$ A $、$ A' $、$ C' $、$ B $四个点组成一个梯形。

(1)当点 $ A $和点 $ C $出发 1 秒后,梯形 $ AA'C'B $的面积是多少平方厘米?
(2)当点 $ A $和点 $ C $出发(
2
)秒后,梯形 $ AA'C'B $的面积是三角形 $ ABC $的 3 倍。
答案:9.
(1)(2+4+2)×4÷2=16(平方厘米) 提示:点A 和点C出发1秒后,向右平移了2厘米,三角形变为一个梯形,梯形的上底是2厘米,下底是(4+2)厘米,高是4厘米,根据梯形的面积=(上底+下底)×高÷2,代入数据计算即可。
(2)2 提示:要使梯形AA'C'B的面积是三角形ABC的3倍,即平行四边形AA'C'C的面积是三角形ABC的2倍,它们的高相同,只要底也相同即可,所以当C'C=BC时,即点A和点C出发4÷2=2(秒)时,梯形AA'C'B的面积是三角形ABC的3倍。
10. 如图,在直角梯形 $ ABCD $中,上底 $ AD = 8 $厘米,高 $ AB = 15 $厘米,三角形 $ BOC $的面积比三角形 $ AOD $的面积大 75 平方厘米,求直角梯形 $ ABCD $的面积。

答案:10.8×15÷2=60(平方厘米) 60+75=135(平方厘米) 135+60=195(平方厘米)
提示:根据“三角形BOC的面积比三角形AOD 的面积大75平方厘米”可知,三角形ABC的面积比三角形ABD的面积大75平方厘米。三角形ABD的面积为8×15÷2=60(平方厘米),则三角形ABC的面积为60+75=135(平方厘米)。由于三角形ABD与三角形ACD同底等高,则它们的面积相等。要求直角梯形ABCD的面积,就是求三角形ABC与三角形ACD的面积和,列式为135+60=195(平方厘米)。