$\begin{cases}72 - 32 - 5 =
35
\\72 - (32 - 5) =
45
\\相差(
10
)\end{cases} $ $\begin{cases}94 - 20 - 10 =
64
\\94 - (20 - 10) =
84
\\相差(
20
)\end{cases} $
[发现]每组算式得数之间的差,是连减算式中最后一个减数的(
2
)倍。
[应用]根据给出的算式填一填。
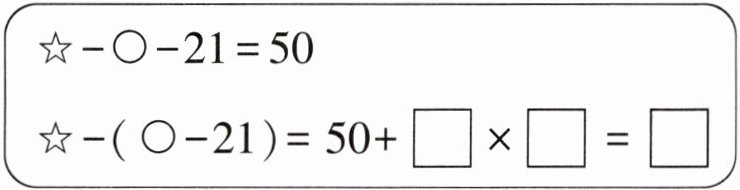
[猜想]如果$a÷b÷6 = 4$,那么$a÷(b÷6) = 4×(
6
×
6
) =
144
$
答案:8. 35 45 10 64 84 20[发现]2[应用]21 2 92[猜想]6 6 144
9. 宁宁从学校步行回家,每分钟走60米。10分钟后,哥哥从学校骑自行车追赶宁宁,在距离学校900米的地方追上了他,哥哥每分钟骑多少米?
答案:9. 900÷(900÷60-10)=180(米)
10. (1)添上小括号,使算式成立。
(7×9 + 12)÷3
= 25
7×(9 + 12)÷3
= 49
(42 + 56)÷7 - 3
= 11
42 + 56÷(7 - 3)
= 56
(2)乐乐今年17岁,爸爸今年49岁,(
9
)年前爸爸的年龄是乐乐的5倍。
(3)用一根绳子绕树3圈余30厘米,如果要绕树5圈则差40厘米,绕树一圈需要绳子(
35
)厘米。
答案:10.
(1)(7×9+12)÷3=25 7×(9+12)÷3=49 (42+56)÷7-3=11 42+56÷(7-3)=56提示:观察第一个式子,首先7×9=63,因此想要得到25,大概还要除以一个3左右的数,因此(7×9+12)÷3=25;观察第二个式子,因为7×7=49,且(9+12)÷3=7,因此7×(9+12)÷3=49;观察第三个式子,可以发现前面的42、56都偏大,因此最终想要得到11,应该要除以7,因此(42+56)÷7-3=11;观察第四个式子,要想得到56,42+14=56,56÷(7-3)=14,因此42+56÷(7-3)=56。
(2)9提示:解决类似的年龄问题,需要注意运用抓不变量法来解决问题。本题中,两人的年龄差是不会随时间的变化而变化的,也就是当爸爸的年龄是乐乐年龄的5倍时,两人的年龄差仍然是49-17=32(岁),可转化为差倍问题求解。(49-17)÷(5-1)=8(岁),17-8=9(年)。
(3)35提示:由题可知,绳子绕树5圈比绕树3圈多用了40+30=70(厘米),这多用的70厘米是因为多绕了5-3=2(圈),所以绕一圈需要用绳子70÷2=35(厘米)。
11. 在乘法算式$A×B$中,如果乘数A减少4,那么积减少48;如果乘数B增加6,那么积增加96。原来的积是(
192
)。
答案:11. 192提示:乘数A减少4,那么积减少48,就是减少了4个B;同理,乘数B增加6,积就增加了6个A。96÷6×(48÷4)=192。
解析:
因为乘数A减少4,积减少48,即减少了4个B,所以$B=48÷4=12$;乘数B增加6,积增加96,即增加了6个A,所以$A=96÷6=16$。原来的积是$A× B=16×12=192$。
192
12. 小宇在计算$32÷8×(76 + □)$时,没有注意到小括号,先算除法,再算乘法,最后加上方框里的数,结果是432。正确答案是(
816
)。
答案:12. 816提示:按照错误的运算顺序,先算出32÷8×76=304,再根据304+□=432,算出方框里的数是128。32÷8×(76+128)=816。
解析:
32÷8×76=4×76=304
432-304=128
32÷8×(76+128)=4×204=816
816
13. 欢欢和乐乐分别从A、B两地同时出发,相向而行,已知欢欢每分钟走50米,乐乐走完全程要30分钟,相向而行10分钟后,两人还差100米才相遇,那么乐乐每分钟走多少米?
答案:13. 50×10+100=600(米) 600÷(30-10)=30(米)提示:10分钟后乐乐没有走的路程是50×10+100=600(米)。600米乐乐要走30-10=20(分钟),每分钟走600÷20=30(米)。
解析:
50×10+100=600(米)
30-10=20(分钟)
600÷20=30(米)
答:乐乐每分钟走30米。