17. (2025·江苏宿迁期末·16分)新趋势推导探究分类讨论是一种非常重要的数学方法,如果一道题所提供的已知条件中包含几种情况,那么我们可以分情况讨论来求解.例如:已知$ |x|= 2 $,$ |y|= 3 $,求代数式$ x+y $的值.情况①:当$ x= 2,y= 3 $时,$ x+y= 5 $;情况②:当$ x= 2,y= -3 $时,$ x+y= -1 $;情况③:当$ x= -2,y= 3 $时,$ x+y= 1 $;情况④:当$ x= -2,y= -3 $时,$ x+y= -5 $.综上所述,代数式$ x+y $的值为5或-1或1或-5.
(1) 已知$ |x+1|= 3 $,则x= ______;
在几何的学习过程中也有类似的情况.
(2) 已知A,B,C三点在同一条直线上,且$ AB= 6,BC= 2 $,求AC的长.
通过分析我们发现,满足题意的情况有两种.
情况①:如图①,当点C在点B的右侧时,AC= ______;
情况②:如图②,当点C在点B的左侧时,AC= ______;
通过以上问题,我们发现,借助画图可以帮助我们更直观地进行分类解答.
(3) 已知数轴上点A和点B表示的数分别是-2和1,C是数轴上一点,且$ BC= 2AB $,则点C表示的数是多少?仿照问题(2),画出图形,结合图形写出分类方法和结果;
(4) 已知O是直线AB上一点,以O为端点画射线OC,OD,使得$ ∠AOC= 60^{\circ} $.若$ OC⊥OD $,求$ ∠BOD $的度数.请画出图形,并写出结果.

答案:(1)-4或2 (2)8 4
(3)满足题意的情况有两种:①如图①,当点C在点B的右侧时,因为点A和点B表示的数分别是-2和1,所以$AB = 3$。因为$BC = 2AB$,所以$BC = 6$,所以点C表示的数是$1 + 6 = 7$;②如图②,当点C在点B的左侧时,同①可得$BC = 6$,所以点C表示的数是$1 - 6 = -5$。综上所述,点C表示的数是7或-5。

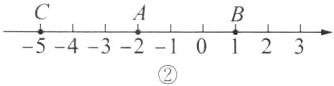
(4)满足题意的情况有两种:①如图③,当OC,OD在直线AB的同侧时,因为$OC\perp OD$,所以$\angle COD = 90^{\circ}$。因为$\angle AOC = 60^{\circ}$,所以$\angle BOD = 180^{\circ}-\angle AOC-\angle COD = 30^{\circ}$;②如图④,当OC,OD在直线AB的异侧时,因为$\angle AOC = 60^{\circ}$,$\angle COD = 90^{\circ}$,所以$\angle AOD = \angle COD-\angle AOC = 30^{\circ}$,所以$\angle BOD = 180^{\circ}-\angle AOD = 150^{\circ}$。综上所述,$\angle BOD$的度数为$30^{\circ}$或$150^{\circ}$。

