答案：【解析】：本题可先根据$D$是$BC$的中点以及$CD$的长度求出$BC$的长度，再结合$AC$与$AB$的关系求出$AB$的长度，最后根据线段的和差关系求出$AD$的长度。
步骤一：求出$BC$的长度
已知$D$是$BC$的中点，根据中点的定义：若点$D$是线段$BC$的中点，则$BC = 2CD$。
因为$CD = 6$，所以$BC = 2×6 = 12$。
步骤二：求出$AB$的长度
由图可知$BC=AC + AB$，又因为$AC = \frac{1}{2}AB$，将$AC = \frac{1}{2}AB$代入$BC=AC + AB$中，可得$BC=\frac{1}{2}AB + AB=\frac{3}{2}AB$。
已知$BC = 12$，即$\frac{3}{2}AB = 12$，两边同时乘以$\frac{2}{3}$，解得$AB = 12×\frac{2}{3}= 8$。
步骤三：求出$AC$的长度
因为$AC = \frac{1}{2}AB$，$AB = 8$，所以$AC = \frac{1}{2}×8 = 4$。
步骤四：求出$AD$的长度
由图可知$AD = CD - AC$，已知$CD = 6$，$AC = 4$，所以$AD = 6 - 4 = 2$。
【答案】：$2$

答案：【解析】：本题主要考查线段的中点性质以及线段的比例关系。
根据已知条件$AM:BM = 1:3$，设$AM = x cm$，则$BM = 3x cm$。
由于$AB = AM + BM$，且$AB = 16 cm$，
所以，$x + 3x = 16$，
合并同类项得$4x = 16$，
解得$x = 4$，
所以，$AM = 4 cm$，$BM = 12 cm$。
因为点P是线段AM的中点，
根据线段中点的性质，中点将线段分为两个等长的部分，
所以，$AP = \frac{1}{2}AM = \frac{1}{2} × 4 = 2 (cm)$。
因为点Q是线段AB的中点，
所以，$AQ = \frac{1}{2}AB = \frac{1}{2} × 16 = 8 (cm)$。
由于$PQ = AQ - AP$，
所以，$PQ = 8 - 2 = 6 (cm)$，
【答案】：$PQ = 6 cm$。

答案：【解析】：
本题主要考察线段长度的计算，需要考虑A、B、C三点的相对位置关系。
当点C位于线段AB上时，可以通过减法来计算AC的长度，即$AC = AB - BC$。
当点C位于线段AB的延长线上时，可以通过加法来计算AC的长度，即$AC = AB + BC$。
【答案】：
当点C位于线段AB上时：
$AC = AB - BC = 3\text{cm} - 2\text{cm} = 1\text{cm}$
当点C位于线段AB的延长线上时：
$AC = AB + BC = 3\text{cm} + 2\text{cm} = 5\text{cm}$
综上，线段AC的长度可以是$1\text{cm}$或者$5\text{cm}$。
故答案为：C. $1\text{cm}$或$5\text{cm}$。

答案：【解析】：
本题主要考查线段长度的计算，需要利用线段的中点性质以及线段之间的比例关系进行计算。
首先，根据题目条件，线段$AB$的长度为12，C是$AB$的中点，因此可以计算出$AC$和$BC$的长度。
其次，根据题目给出的$AB = 3AD$，可以求出$AD$的长度。
最后，需要分两种情况讨论点D的位置（在点A的左侧或右侧），并分别计算出$CD$的长度。
【答案】：
解：
∵ $AB = 12$，C是$AB$的中点，
∴ $AC = \frac{1}{2}AB = 6$。
∵ $AB = 3AD$，
∴ $AD = \frac{1}{3}AB = 4$。
当点D在点A的左侧时，
$CD = AC + AD = 6 + 4 = 10$；
当点D在点A的右侧时，
$CD = AC - AD = 6 - 4 = 2$。
∴ $CD$的长度为$2$或$10$。

答案：【解析】：
本题可根据折叠的性质以及平角的定义来求解$∠2$的度数。
步骤一：明确折叠的性质
折叠前后对应角相等，所以由折叠可知$∠1$与它折叠前的对应角相等。
步骤二：根据平角的定义列方程
观察图形可知，$∠1$、$∠2$以及$∠1$折叠前的对应角组成了一个平角，因为平角的度数为$180^{\circ}$，且$∠1$与它折叠前的对应角相等，都为$65^{\circ}$，所以可列出方程$∠1 + ∠2 + ∠1$折叠前的对应角$ = 180^{\circ}$，即$65^{\circ} + ∠2 + 65^{\circ} = 180^{\circ}$。
步骤三：解方程求出$∠2$的度数
对$65^{\circ} + ∠2 + 65^{\circ} = 180^{\circ}$进行求解，先计算$65^{\circ}+65^{\circ}=130^{\circ}$，则方程变为$130^{\circ} + ∠2 = 180^{\circ}$，两边同时减去$130^{\circ}$可得$∠2 = 180^{\circ} - 130^{\circ} = 50^{\circ}$。
【答案】：
$50^{\circ}$

答案：1. 设$\angle BFE = x$：
因为$\angle BFC'$比$\angle BFE$大$6^{\circ}$，所以$\angle BFC'=x + 6^{\circ}$。
由折叠可知$\angle CFE=\angle C'FE$。
又因为$\angle CFE+\angle C'FE+\angle BFC' = 180^{\circ}$（平角的定义），且$\angle CFE=\angle C'FE$，所以$2\angle CFE+\angle BFC' = 180^{\circ}$，即$2\angle CFE+x + 6^{\circ}=180^{\circ}$，那么$2\angle CFE=174^{\circ}-x$，$\angle CFE = 87^{\circ}-\frac{x}{2}$。
同时，$\angle BFE+\angle CFE = 180^{\circ}$（平角的定义），即$x+\angle CFE = 180^{\circ}$。
2. 把$\angle CFE = 87^{\circ}-\frac{x}{2}$代入$x+\angle CFE = 180^{\circ}$：
得$x+(87^{\circ}-\frac{x}{2}) = 180^{\circ}$。
去括号：$x + 87^{\circ}-\frac{x}{2}=180^{\circ}$。
移项：$x-\frac{x}{2}=180^{\circ}-87^{\circ}$。
合并同类项：$\frac{x}{2}=93^{\circ}$，解得$x = 62^{\circ}$。
3. 求$\angle CFE$的值：
因为$\angle BFE+\angle CFE = 180^{\circ}$，$\angle BFE = 62^{\circ}$。
所以$\angle CFE=180^{\circ}-\angle BFE$。
则$\angle CFE = 118^{\circ}$。
故答案为$118^{\circ}$。

答案：【解析】：
本题主要考查了角的平分线的性质，即角的平分线将角分为两个相等的小角。
首先，根据题目给出的信息，$OM$是$\angle AOB$的平分线，$ON$是$\angle BOC$的平分线。
当$OC$在$\angle AOB$内部时：
由于$OM$是$\angle AOB$的平分线，所以$\angle BOM = \frac{1}{2} \angle AOB = \frac{1}{2} × 80^{\circ} = 40^{\circ}$。
同理，$ON$是$\angle BOC$的平分线，所以$\angle BON = \frac{1}{2} \angle BOC = \frac{1}{2} × 20^{\circ} = 10^{\circ}$。
因此，$\angle MON = \angle BOM - \angle BON = 40^{\circ} - 10^{\circ} = 30^{\circ}$。
当$OC$在$\angle AOB$外部时：
同样，由于$OM$是$\angle AOB$的平分线，所以$\angle BOM = \frac{1}{2} \angle AOB = 40^{\circ}$。
$ON$是$\angle BOC$的平分线，所以$\angle BON = \frac{1}{2} \angle BOC = 10^{\circ}$，但此时$\angle BON$在$\angle BOM$的外部，
因此，$\angle MON = \angle BOM + \angle BON = 40^{\circ} + 10^{\circ} = 50^{\circ}$。
综合以上两种情况，得出$\angle MON$的度数有两种可能，即$30^{\circ}$或$50^{\circ}$。
【答案】：D. $50^{\circ}或30^{\circ}$。

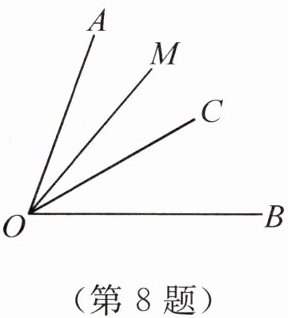
答案：解：由图可知，OC在∠AOB内部。
∵∠AOB=70°，∠BOC=30°，
∴∠AOC=∠AOB - ∠BOC=70° - 30°=40°。
∵OM平分∠AOC，
∴∠AOM=∠COM=∠AOC÷2=40°÷2=20°。
∴∠BOM=∠COM + ∠BOC=20° + 30°=50°。
50°

答案：解：
∵直线AB,CD相交于点O，
∴∠AOC=∠BOD=β（对顶角相等）。
∵OE平分∠BOD，
∴∠BOE=∠DOE=β/2。
∵∠COE+∠DOE=180°（邻补角定义），
∴∠COE=180°-β/2。
∵OF平分∠COE，
∴∠COF=∠EOF=∠COE/2=90°-β/4。
∵∠AOC+∠COF+∠FOG=180°（平角定义），且OG⊥OF，∠FOG=90°，
∴β+(90°-β/4)+90°+∠BOG=180°（∠AOB为平角）。
化简得：∠BOG=β/4。
答案：β/4

答案：【解析】：根据题意，已知$AB=12km$，$BC=5km$，$\angle ABG=48^\circ$，$\angle CBE=42^\circ$，
由于$BE// AG$，所以$\angle ABG+\angle BAG=180^\circ$，
那么$\angle BAG=180^\circ-48^\circ=132^\circ$，
$\angle ABC=180^\circ-\angle ABG-\angle CBE=180^\circ-48^\circ-42^\circ=90^\circ$，
由于$\angle ABC=90^\circ$，所以$AB\perp BC$，
A地到公路BC的距离就是AB的长度，即$12km$。
【答案】：B。