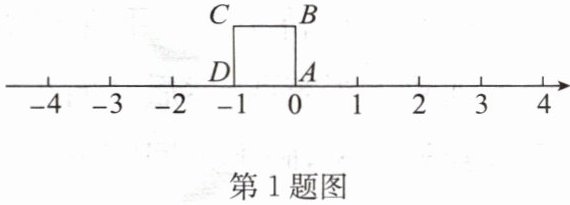
1. 边长为1个单位长度的正方形纸片ABCD在数轴上的位置如图所示,点A,D对应的数分别为0和-1. 把正方形纸片ABCD绕着顶点在数轴上向右滚动(无滑动),在滚动过程中经过数轴上的数2023的是 (
D
)
A.点A
B.点B
C.点C
D.点D
答案:D
解析:
解:正方形边长为1,初始位置A(0),D(-1),B(1),C(0)。
滚动规律:每滚动4次(周长4),点的对应数循环。
滚动1次(绕A):D(0),C(1),B(0),A(1);
滚动2次(绕B):A(2),D(1),C(2),B(3);
滚动3次(绕C):B(4),A(3),D(4),C(5);
滚动4次(绕D):C(6),B(5),A(6),D(7);
循环周期为4,对应数依次为D(0,4,8...),C(1,5,9...),B(2,6,10...),A(3,7,11...)。
2023÷4=505...3,余数3对应A。
答案:A
2. 一个小球落在数轴上的点$P_{0}$处,第一次从点$P_{0}$向左跳1个单位长度到点$P_{1}$,第二次从点$P_{1}$向右跳2个单位长度到点$P_{2}$,第三次从点$P_{2}$向左跳3个单位长度到点$P_{3}$,第四次从点$P_{3}$向右跳4个单位长度到点$P_{4}$,…,若小球从原点出发,按以上规律跳了6次时,它落在数轴上的点$P_{6}$所表示的数是
3
;若小球按以上规律跳了2n次时,它落在数轴上的点$P_{2n}$所表示的数恰好是n+2,则这个小球的初始位置点$P_{0}$所表示的数是
2
.
答案:3 2
解析:
第一空:
解:小球从原点出发,即初始位置$P_0 = 0$。
第1次跳:$P_1 = 0 - 1 = -1$
第2次跳:$P_2 = -1 + 2 = 1$
第3次跳:$P_3 = 1 - 3 = -2$
第4次跳:$P_4 = -2 + 4 = 2$
第5次跳:$P_5 = 2 - 5 = -3$
第6次跳:$P_6 = -3 + 6 = 3$
第二空:
解:设初始位置$P_0 = x$。
跳$2n$次的位置为:
$P_{2n} = x - 1 + 2 - 3 + 4 - \dots - (2n-1) + 2n$
分组计算:$(-1+2) + (-3+4) + \dots + [-(2n-1)+2n] = n$
则$P_{2n} = x + n$。
由题意$x + n = n + 2$,解得$x = 2$。
答案:3;2
3. 如图,在纸面上有一条数轴,折叠纸面.
(1)若表示1的点与表示-1的点重合,则表示-2的点与表示
2
的点重合;
(2)若表示-2的点与表示4的点重合,解答以下问题:
①表示5的点与表示
-3
的点重合;
②若数轴上A,B两点之间的距离为9(点A在点B的左侧),且A,B两点经折叠后重合,求A,B两点表示的数.
解:由题意,得A,B两点与对称中心的距离均为9÷2=4.5,且对称中心是表示数1的点,
所以A,B两点表示的数分别是-3.5,5.5.
答案:(1)2
(2)①-3
②解:由题意,得A,B两点与对称中心的距离均为9÷2=4.5,且对称中心是表示数1的点,
所以A,B两点表示的数分别是-3.5,5.5.