1. 十八世纪瑞士数学家欧拉证明了简单多面体的顶点数$(V)$、面数$(F)$、棱数$(E)$之间存在的一个有趣的关系式,被称为欧拉公式. 请你观察下列如图①所示的五种简单多面体模型,解答下列问题:
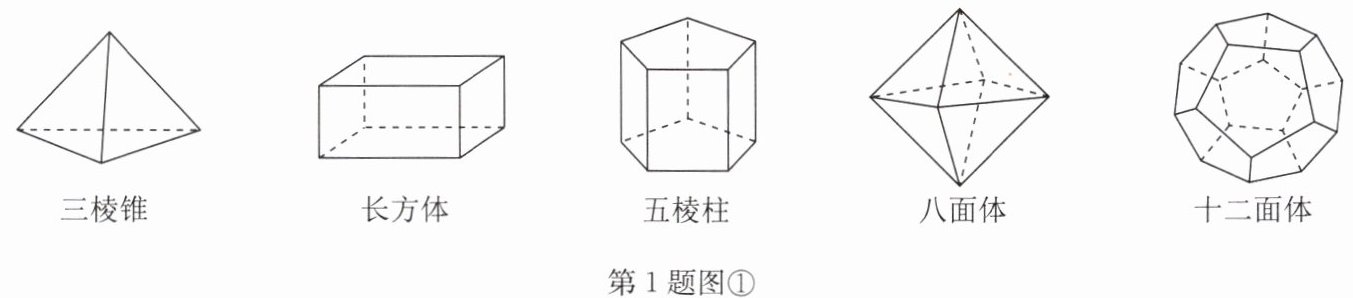
【观察总结】(1)五种简单多面体的顶点数$(V)$、面数$(F)$、棱数$(E)$如下表:
|多面体|顶点数$(V)$|面数$(F)$|棱数$(E)$|
|三棱锥|4|4|6|
|长方体|8|6|12|
|五棱柱|10|7|15|
|八面体|6|8|12|
|十二面体|20|12|30|
猜想顶点数$(V)$、面数$(F)$、棱数$(E)$之间存在的关系式是
V+F−E=2
. (用所给的字母表达)
【简单应用】(2)能否组成一个有24条棱、10个面、13个顶点的多面体?请说明理由.
解:不能,理由:因为10+13−24=−1≠2,所以不能组成一个有24条棱、10个面、13个顶点的多面体.
(3)一个正二十面体有30条棱,则它的顶点数是
12
.
【实践探究】(4)学校校园文化节,七年级数学实践小组同学制作了各种各样的多面体作品.
①一个多面体作品,只有12个顶点,并且过每个顶点都有4条棱,则这个多面体的面数是
14
;
②一个多面体作品如图②所示,每个面的形状是正三角形或正五边形,每条棱都是正三角形和正五边形的公共边,则该多面体作品正三角形比正五边形的面数多
8
个.
