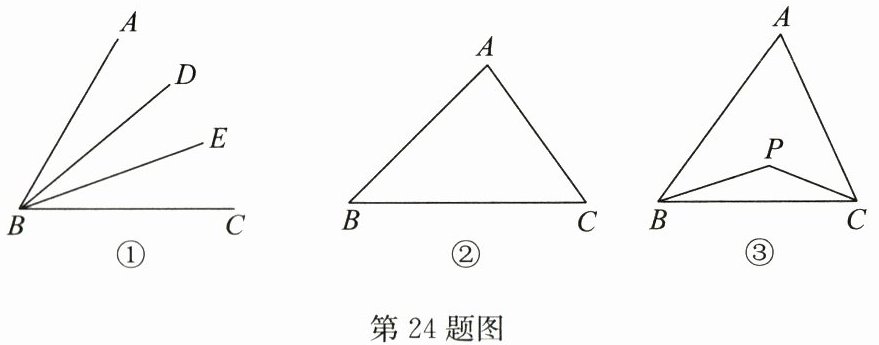
24. (12分)(2024春·武进区月考)【概念认识】
如图①,在$∠ABC$中,若$∠ABD= ∠DBE= ∠EBC$,则$BD$,$BE叫作∠ABC$的“三分线”.其中,$BD$是“邻$AB$三分线”,$BE$是“邻$BC$三分线”.
【问题解决】
(1)如图②,在$\triangle ABC$中,$∠A= 80^{\circ }$,$∠B= 45^{\circ }$,若$∠B的三分线BD交AC于点D$,求$∠BDC$的度数;
(2)如图③,在$\triangle ABC$中,$BP$,$CP分别是∠ABC$的“邻$BC$三分线”和$∠ACB$的“邻$BC$三分线”,且$∠BPC= 140^{\circ }$,求$∠A$的度数;
【延伸推广】
(3)在$\triangle ABC$中,$∠ACD是\triangle ABC$的外角,$∠B的三分线所在的直线与∠ACD的三分线所在的直线交于点P$.若$∠A= m^{\circ }(m>54)$,$∠B= 54^{\circ }$,直接写出$∠BPC$的度数.(用含$m$的代数式表示)
答案:解:(1)如答图①。
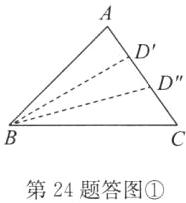
当 $BD$ 是“邻 $AB$ 三分线”时,$\angle ABD' = \frac{1}{3}\angle ABC = 15^{\circ}$,$\therefore \angle BD'C = 80^{\circ} + 15^{\circ} = 95^{\circ}$;当 $BD$ 是“邻 $BC$ 三分线”时,$\angle ABD'' = \frac{2}{3}\angle ABC = 30^{\circ}$,$\therefore \angle BD''C = 80^{\circ} + 30^{\circ} = 110^{\circ}$。$\therefore \angle BDC$ 的度数为 $95^{\circ}$ 或 $110^{\circ}$。
(2)在 $\triangle BPC$ 中,$\because \angle BPC = 140^{\circ}$,$\therefore \angle PBC + \angle PCB = 40^{\circ}$。又 $\because BP,CP$ 分别是 $\angle ABC$ 的“邻 $BC$ 三分线”和 $\angle ACB$ 的“邻 $BC$ 三分线”,$\therefore \angle PBC = \frac{1}{3}\angle ABC,\angle PCB = \frac{1}{3}\angle ACB$,$\therefore \frac{1}{3}\angle ABC + \frac{1}{3}\angle ACB = 40^{\circ}$,$\therefore \angle ABC + \angle ACB = 120^{\circ}$。在 $\triangle ABC$ 中,$\angle A + \angle ABC + \angle ACB = 180^{\circ}$,$\therefore \angle A = 180^{\circ} - (\angle ABC + \angle ACB) = 60^{\circ}$。
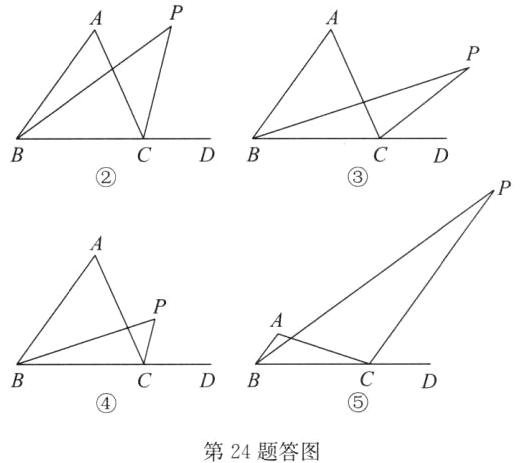
(3) $\angle BPC$ 的度数为 $\frac{2}{3}m^{\circ}$ 或 $\frac{1}{3}m^{\circ}$ 或 $\frac{2}{3}m^{\circ} + 18^{\circ}$ 或 $\frac{1}{3}m^{\circ} - 18^{\circ}$ 点拨:分 4 种情况进行讨论:情况一:如答图②,当 $BP$ 和 $CP$ 分别是“邻 $AB$ 三分线”“邻 $AC$ 三分线”时,$\angle PBD = \frac{2}{3}\angle ABC = 36^{\circ},\angle PCD = \frac{2}{3}\angle ACD = \frac{2}{3}(\angle A + \angle ABC) = \frac{2}{3}m^{\circ} + 36^{\circ}$,$\therefore \angle BPC = \angle PCD - \angle PBD = \frac{2}{3}m^{\circ}$;情况二:如答图③,当 $BP$ 和 $CP$ 分别是“邻 $BC$ 三分线”“邻 $CD$ 三分线”时,$\angle PBD = \frac{1}{3}\angle ABC = 18^{\circ}$,$\angle PCD = \frac{1}{3}\angle ACD = \frac{1}{3}m^{\circ} + 18^{\circ}$,$\therefore \angle BPC = \angle PCD - \angle PBD = \frac{1}{3}m^{\circ}$;情况三:如答图④,当 $BP$ 和 $CP$ 分别是“邻 $BC$ 三分线”“邻 $AC$ 三分线”时,同理得 $\angle BPC = \angle PCD - \angle PBD = \frac{2}{3}m^{\circ} + 18^{\circ}$;情况四:如答图⑤,当 $BP$ 和 $CP$ 分别是“邻 $AB$ 三分线”“邻 $CD$ 三分线”时,同理得 $\angle BPC = \angle PCD - \angle PBD = \frac{1}{3}m^{\circ} - 18^{\circ}$。综上所述,$\angle BPC$ 的度数为 $\frac{2}{3}m^{\circ}$ 或 $\frac{1}{3}m^{\circ}$ 或 $\frac{2}{3}m^{\circ} + 18^{\circ}$ 或 $\frac{1}{3}m^{\circ} - 18^{\circ}$。