4. 如图是一条直线和直线外一点A。
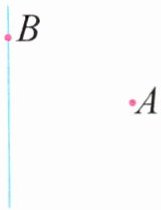
(1) 量出点A到直线的距离是( )毫米。
(2) 过直线上的点B画该直线的垂线。
(3) 以B为顶点,引一条射线与已知直线组成$125^{\circ}$的角。
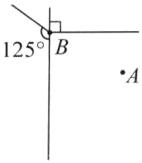
答案:(1) 13 (2)(3) 如图。(角的画法不唯一)
5. 新情境 真实生活 奇奇和妙妙一起在电脑上玩架梯子游戏,两人的梯子长度相等,将梯子一端靠在墙上,游戏界面显示妙妙的梯子与地面的角度为$62^{\circ}$(如图),要使奇奇的梯子与地面的角度为$70^{\circ}$,请你在图中画出奇奇的梯子,奇奇和妙妙谁的梯子架得高?

答案:奇奇的梯子如下图。通过画图可知,奇奇的梯子架得高。

6. 度量一个角,角的一条边对着量角器上$180^{\circ}$刻度线,另一条边对着$60^{\circ}$刻度线,这个角的度数可能是(
60°或120°
)。
答案:60°或120°
解析:
解:情况一:若角的一条边对着量角器外圈$180^{\circ}$刻度线,另一条边对着外圈$60^{\circ}$刻度线,这个角的度数为$180^{\circ}-60^{\circ}=120^{\circ}$;
情况二:若角的一条边对着量角器内圈$180^{\circ}$刻度线,另一条边对着内圈$60^{\circ}$刻度线,这个角的度数为$180^{\circ}-60^{\circ}=120^{\circ}$;
情况三:若角的一条边对着量角器外圈$180^{\circ}$刻度线,另一条边对着内圈$60^{\circ}$刻度线,此时外圈$180^{\circ}$刻度线对应内圈$0^{\circ}$刻度线,这个角的度数为$60^{\circ}-0^{\circ}=60^{\circ}$;
情况四:若角的一条边对着量角器内圈$180^{\circ}$刻度线,另一条边对着外圈$60^{\circ}$刻度线,此时内圈$180^{\circ}$刻度线对应外圈$0^{\circ}$刻度线,这个角的度数为$60^{\circ}-0^{\circ}=60^{\circ}$。
综上,这个角的度数可能是$60^{\circ}$或$120^{\circ}$。
答案:$60^{\circ}$或$120^{\circ}$
由于题目中包含图片链接,无法直接查看图片中的答题空位置。若图片中的题目存在三个依次排列的填空处(如( )、____等),则填入答案后的题目内容应为:7.
165
90
40
(注:此处假设图片中三个填空位置依次对应三个答案,具体需根据实际图片中的答题空位置调整答案填入顺序)。
答案:165 90 40
解析:
∠1=(165)°
∠2=(90)°
∠3=(40)°
8. (南京江北新区期末)如图,河流在两个村庄A、B的附近,可以近似地看成是折线段(图中l),A、B分别在河的两旁。现要在河边修建一个水泵站,同时向A、B两村供水,为了节约建设的费用,就要使所铺设的管道最短。甲提出了这样的建议:从B向河道作垂线交l于点P,则点P为水泵站的位置。
(1) 你是否同意甲的建议?( )(填“是”或“否”)
(2) 若同意,请说明理由,若不同意,则你认为水泵站应该建在哪里?请在图中画出来,并说明依据。

答案:(1) 否 (2) 如图,水泵站应该建在点P'处,依据:两点之间,线段最短。

9. 新素养 几何直观

如图,共端点A的射线a与d,b与e,c与f分别垂直,c与d的夹角是(
15
)$^{\circ}$。
答案:15 解析 c与f垂直,e与f的夹角是45°,则c与e的夹角是90°-45°=45°,由于b与e垂直,那么b与c的夹角是90°-45°=45°。又因为a与d垂直,那么c与d的夹角为90°-45°-30°=15°。
10. 把一张长方形纸折成如下图的形状,已知$∠1+∠2+∠3= 220^{\circ}$,$∠4= 20^{\circ}$,求$∠1$、$∠2$、$∠3和∠5$的度数。

答案:∠1=220°-180°=40° ∠3=∠1=40° ∠2=180°-40°=140° ∠5=90°-20°×2=50° 解析 由题图可知,∠2+∠3=180°,根据“∠1+∠2+∠3=220°”可得出∠1=220°-180°=40°;根据∠1+∠2=180°和∠2+∠3=180°可得出∠3=∠1=40°,∠2=180°-40°=140°;又根据2∠4+∠5=90°,所以∠5=90°-20°×2=50°。
解析:
由题图可知:
∠2 + ∠3 = 180°,
因为∠1 + ∠2 + ∠3 = 220°,所以∠1 = 220° - (∠2 + ∠3) = 220° - 180° = 40°;
因为∠1 + ∠2 = 180°,所以∠2 = 180° - ∠1 = 180° - 40° = 140°;
因为∠2 + ∠3 = 180°,所以∠3 = 180° - ∠2 = 180° - 140° = 40°;
由折叠性质知,2∠4 + ∠5 = 90°,∠4 = 20°,所以∠5 = 90° - 2×20° = 50°。
∠1 = 40°,∠2 = 140°,∠3 = 40°,∠5 = 50°。