26. (9分)如图甲所示,小明在探究光的折射现象时,将一束入射角为50°的光线斜射入杯中,在杯底形成光斑,然后逐渐往杯中加水,观察杯底光斑的位置变化.他对实验中光偏折程度的差异产生了兴趣.为了定量反映这种差异,他将“折射角与入射角的比值”定义为“偏折比”.根据所学知识和生活经验,小明对影响“偏折比”大小的因素提出如下猜想.
猜想1:与液体深度有关.
猜想2:与液体种类有关.
猜想3:与入射光的颜色有关.
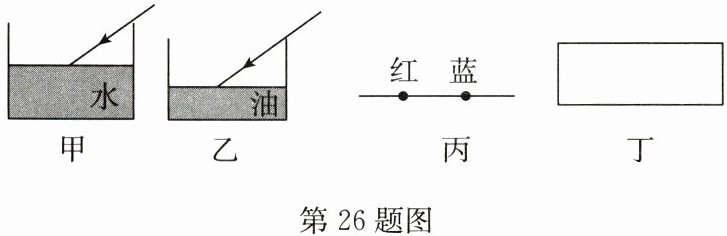
(1)图甲实验中,加水过程中,杯底光斑将向
右
(选填“左”或“右”)移动.你认为猜想1
错误
(选填“正确”或“错误”),理由是
液体深度改变,入射角、折射角的大小不变,偏折比不变
.
(2)为了探究猜想2,小明只将图甲中的水换成油,当油的深度小于水的深度(如图乙所示),杯底光斑位置恰与图甲实验时光斑位置重合.对比可知:在相同条件下,油对光的“偏折比”比水对光的“偏折比”
小
(选填“大”或“小”).
(3)为了探究猜想3,小明用图甲装置先后入射红、蓝色激光,杯底光斑位置如图丙所示,则
红
光的“偏折比”大.
(4)将一束激光穿过如图丁所示的玻璃砖,若光在玻璃砖上表面折射时的“偏折比”为0.8,则光在下表面折射时的“偏折比”为
1.25
.
(5)根据小明的操作和计算结果,小华认为,应该将“偏折比”定义为“光线在空气中与法线的夹角α和光线在介质中与法线的夹角β之比”.经过对多组不同玻璃砖的实验,测得数据如表所示.
| | 玻璃砖A | 玻璃砖B | 玻璃砖C |
| 光线在空气中与法线夹角α | 30.0° 45.0° 60.0° | 30.0° 45.0° 60.0° | 30.0° 45.0° 60.0° |
| 光线在玻璃中与法线夹角β | 22.0° 32.0° 40.5° | 17.0° 24.4° 30.4° | 20.0° 28.9° 36.3° |
| $\frac{\alpha}{\beta}$ | 1.36 1.41 1.48 | 1.76 1.84 1.97 | 1.50 1.58 1.65 |
根据表格中的数据,分析可得:光在空气与另一种透明介质中传播时,对于不同的入射角,“偏折比”
不相等
(选填“相等”或“不相等”);对于相同的入射角,“偏折比”越大,介质对光的折射程度越
高
(选填“高”或“低”),因此我们认为小华对“偏折比”定义的优点是
能反映不同介质对光的折射程度(合理即可)
.