2025年启东中学作业本八年级数学上册江苏版第112页解析答案

12.(10分)(2023春·武进区校级月考)在平面直角坐标系中,$P(a,b)$是第一象限内一点,给出如下定义:$k_{1}=\frac {a}{b}$和$k_{2}=\frac {b}{a}$两个值中的最大值叫作点P的“倾斜系数”k.
(1)点$P(6,2)$的“倾斜系数”k的值为____

;
(2)若点$P(a,b)$的“倾斜系数”$k=2$,且$a+b=3$,求OP的长.
解: ∵ 点 $P ( a, b )$ 的 “倾斜系数” $k = 2$,
$ \therefore \frac { a } { b } = 2$ 或 $ \frac { b } { a } = 2$,
即 $a = 2 b$ 或 $b = 2 a$,
∵ $a + b = 3$,
$ \therefore \left\{ \begin{array} { l } { a = 1, } \\ { b = 2 } \end{array} \right. $ 或 $ \left\{ \begin{array} { l } { a = 2, } \\ { b = 1, } \end{array} \right. $
$ \therefore O P = \sqrt { a ^ { 2 } + b ^ { 2 } } = $____

$\sqrt{5}$

答案：(1) 3
(2) 解: ∵ 点 $P ( a, b )$ 的 “倾斜系数” $k = 2$,
$ \therefore \frac { a } { b } = 2$ 或 $ \frac { b } { a } = 2$,
即 $a = 2 b$ 或 $b = 2 a$,
∵ $a + b = 3$,
$ \therefore \left\{ \begin{array} { l } { a = 1, } \\ { b = 2 } \end{array} \right. $ 或 $ \left\{ \begin{array} { l } { a = 2, } \\ { b = 1, } \end{array} \right. $
$ \therefore O P = \sqrt { a ^ { 2 } + b ^ { 2 } } = \sqrt { 5 } $.

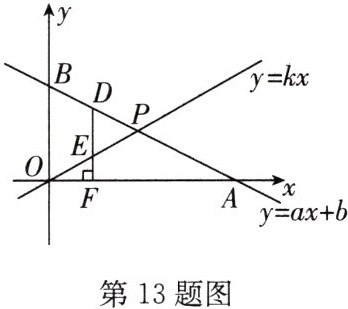
13.(12分)如图,在平面直角坐标系中,一次函数$y=ax+b$的图象与x轴、y轴分别交于点A,B,与直线$y=kx$交于点$P(2,1)$,且$PO=PA$.
(1)求点A的坐标和k的值;
(2)求a,b的值;
(3)点D为直线$y=ax+b$上一动点,其横坐标为$m(m＜2),DF⊥x$轴于点F,交直线$y=kx$于点E,且$DF=3EF$,求点D的坐标.

答案：
解: (1) 如答图, 作 $P Q \perp O A$ 于点 $Q$.

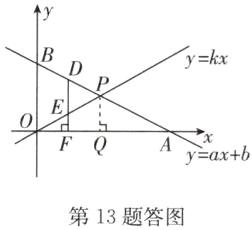
∵ $P O = P A$, $P Q \perp O A$, $P ( 2, 1 )$,
$ \therefore O Q = Q A = 2$, $ \therefore O A = 4$, $ \therefore A ( 4, 0 ) $.
把 $P ( 2, 1 )$ 代入 $y = k x$ 中得 $2 k = 1$,
$ \therefore k = \frac { 1 } { 2 } $.
(2) 把 $A ( 4, 0 )$, $P ( 2, 1 )$ 代入 $y = a x + b$ 得
$ \left\{ \begin{array} { l } { 4 a + b = 0, } \\ { 2 a + b = 1, } \end{array} \right. $ 解得 $ \left\{ \begin{array} { l } { a = - \frac { 1 } { 2 }, } \\ { b = 2. } \end{array} \right. $
(3) 由 (1) (2) 可得 $D \left( m, - \frac { 1 } { 2 } m + 2 \right)$, $E \left( m, \frac { 1 } { 2 } m \right)$, $F ( m, 0 )$,
$ \therefore D F = \left| - \frac { 1 } { 2 } m + 2 \right|$, $E F = \left| \frac { 1 } { 2 } m \right|$.
∵ $D F = 3 E F$, $ \therefore \left| - \frac { 1 } { 2 } m + 2 \right| = 3 \left| \frac { 1 } { 2 } m \right|$,
当 $ - \frac { 1 } { 2 } m + 2 = 3 \times \frac { 1 } { 2 } m$ 时, 解得 $m = 1$,
$ \therefore D \left( 1, \frac { 3 } { 2 } \right)$;
当 $ - \frac { 1 } { 2 } m + 2 = - 3 \times \frac { 1 } { 2 } m$ 时, 解得 $m = - 2$,
$ \therefore D ( - 2, 3 )$.
综上可知, 点 $D$ 的坐标为 $ \left( 1, \frac { 3 } { 2 } \right)$ 或 $ ( - 2, 3 ) $.