10.「2025广东广州期中」(10分)如图,AB是$\odot O$的直径,四边形ABCD内接于$\odot O$,OD交AC于点E,$\overset{\frown }{AD}= \overset{\frown }{CD}$.
(1)求证:$OD// BC$.
证明: ∵ $\overparen{AD} = \overparen{CD}$, ∴ OD ⊥ AC, 又 ∵ AB 是⊙O 的直径, ∴ ∠ACB = 90°, 即 BC ⊥ AC, ∴ OD // BC.
(2)若$AC= 10,DE= 4$,求BC的长.
解:∵ $\overparen{AD} = \overparen{CD}$, ∴ OD ⊥ AC 于点 E 且 AE = CE, 又 ∵ AC = 10, ∴ AE = CE = $\frac{1}{2}$AC = 5, 设⊙O 半径为 R, 则 OA = R, OE = R - 4, 在 Rt△AOE 中, $OA^{2} = OE^{2} + AE^{2}$, 即 $R^{2} = (R - 4)^{2} + 5^{2}$, ∴ $R = \frac{41}{8}$, 又 ∵ 点 O, E 分别是 AB, AC 的中点, ∴ $OE = \frac{1}{2}$BC, ∴ $BC = 2OE = 2×(\frac{41}{8} - 4) =$
$\frac{9}{4}$
.
答案:解析 (1) 证明: ∵ $\overparen{AD} = \overparen{CD}$, ∴ OD ⊥ AC, 又 ∵ AB 是⊙O 的直径, ∴ ∠ACB = 90°, 即 BC ⊥ AC, ∴ OD // BC. (2) ∵ $\overparen{AD} = \overparen{CD}$, ∴ OD ⊥ AC 于点 E 且 AE = CE, 又 ∵ AC = 10, ∴ AE = CE = $\frac{1}{2}$AC = 5, 设⊙O 半径为 R, 则 OA = R, OE = R - 4, 在 Rt△AOE 中, $OA^{2} = OE^{2} + AE^{2}$, 即 $R^{2} = (R - 4)^{2} + 5^{2}$, ∴ $R = \frac{41}{8}$, 又 ∵ 点 O, E 分别是 AB, AC 的中点, ∴ $OE = \frac{1}{2}$BC, ∴ $BC = 2OE = 2×(\frac{41}{8} - 4) = \frac{9}{4}$.
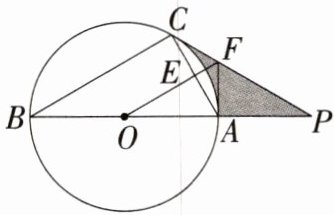
11.「2025四川广安期中」(14分)如图,$\triangle ABC内接于\odot O$,AB是直径,切线PC切$\odot O$于C,交BA的延长线于点P,$OF// BC$交AC于点E,交PC于点F.
(1)写出OF与AC的位置关系:______.
(2)求证:AF是$\odot O$的切线.
(3)若$AC= 6,∠B= 30^{\circ }$,求阴影部分的面积.
答案:解析 (1) OF ⊥ AC. (2) 证明: 连接 OC,

∵ PC 为圆 O 切线, ∴ CP ⊥ OC, ∴ ∠OCP = 90°, ∵ OF // BC, ∴ ∠AOF = ∠B, ∠COF = ∠OCB, ∵ OC = OB, ∴ ∠OCB = ∠B, ∴ ∠AOF = ∠COF, ∵ 在 △AOF 和 △COF 中, $\begin{cases}OA = OC, \\ ∠AOF = ∠COF, \\ OF = OF,\end{cases}$ ∴ △AOF ≌ △COF(SAS), ∴ ∠OAF = ∠OCF = 90°, 又 ∵ OA 为圆 O 的半径, ∴ AF 为圆 O 的切线. (3) ∵ AB 为直径, ∴ ∠BCA = 90°, ∵ AC = 6, ∠B = 30°, ∴ AB = 12, ∠BAC = 60°, ∴ OA = OB = OC = AC = 6, ∴ △AOC 是等边三角形, ∴ ∠AOC = 60°, ∵ ∠OCP = 90°, ∴ CP = $\sqrt{3}$OC = $6\sqrt{3}$, ∴ $S_{△OCP} = \frac{1}{2}$OC · CP = $\frac{1}{2}$×6×$6\sqrt{3}$ = $18\sqrt{3}$, $S_{扇形AOC} = \frac{60·π×6^{2}}{360} = 6π$, ∴ $S_{阴影} = S_{△OCP} - S_{扇形AOC} = 18\sqrt{3} - 6π$.
12.(16分)阅读材料,并完成相应任务.
问题背景:《阿基米德全集》中记述了古希腊伟大的数学家、哲学家、物理学家阿基米德提出的关于圆的一些问题,其中有这样一个问题:如图1,AB和BC是$\odot O$的两条弦(即折线ABC是圆的一条折弦),$BC>AB$,点M是$\overset{\frown }{ABC}$的中点,则从点M向BC所作垂线的垂足D是折弦ABC的中点,即$CD= DB+BA$.
(1)如图2,牛牛同学尝试运用“截长法”说明“$CD= DB+BA$”,他在CD上截取$CE= BA$,连接MA,MB,ME,MC,请根据牛牛的思路完成证明过程.
(2)如图3,在$\odot O$中,$\overset{\frown }{BD}= \overset{\frown }{CD},DE⊥AC$,若$AB= 3,AC= 7$,则$AE= $
2
.
答案:解析 (1) ∵ ∠A 与 ∠C 都是 $\overparen{MB}$ 所对的圆周角, ∴ ∠A = ∠C, ∵ M 是 $\overparen{ABC}$ 的中点, ∴ MA = MC. 在 △MBA 和 △MEC 中, $\begin{cases}MA = MC, \\ ∠A = ∠C, \\ AB = CE,\end{cases}$ ∴ △MBA ≌ △MEC(SAS), ∴ MB = ME. ∵ MD ⊥ BC, ∴ DB = DE, ∴ CE + ED = BA + DB, 即 CD = BA + DB. (2) ∵ $\overparen{BD} = \overparen{CD}$, DE ⊥ AC, ∴ CE = AE + AB, ∵ AB = 3, AC = 7, ∴ CE = $\frac{1}{2}$(AB + AC) = 5, ∴ AE = AC - CE = 2.