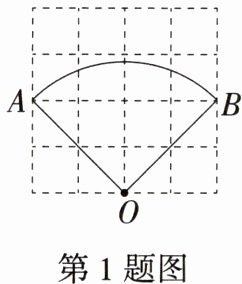
1.「2025陕西西安阎良期末」如图,在4×4的方格中,每个小方格都是边长为1的正方形,O,A,B分别是小正方形的顶点,则扇形OAB的面积等于(
A
)
A.2π
B.√2π
C.2√2π
D.√2/2π
答案:A 由题意可知,$\angle AOB = 90^{\circ}$,$OA = 2\sqrt{2}$,
$\therefore$ 扇形 $OAB$ 的面积等于 $\frac{90\pi \times (2\sqrt{2})^{2}}{360} = 2\pi$。故选 A。
2.「2024浙江杭州拱墅二模」已知一个扇形的面积是12π,弧长是2π,则这个扇形的半径为(
C
)
A.24
B.36
C.12
D.6
答案:C 由 $S = \frac{1}{2}lr$,得 $12\pi = \frac{1}{2} \times 2\pi \cdot r$,解得 $r = 12$。故选 C。
3.「2024天津河西期末」一个扇形的半径为24 cm,面积是$240π cm^2,$则扇形的圆心角为(
D
)
A.300°
B.240°
C.180°
D.150°
答案:D 设扇形的圆心角为 $n^{\circ}$,则 $\frac{n\pi \times 24^{2}}{360} = 240\pi$,解得 $n = 150$。故选 D。
4.如图,有一根6 m长的绳子,一端拴在围墙墙角的柱子上,另一端拴着小羊M(羊只能在草地上活动,体积忽略不计),那么小羊M在草地上的最大活动区域的面积是( )
$A.9π m^2$
$B.29/3π m^2$
$C.15π m^2$
$D.31/3π m^2$

答案:B 如图,扇形 $AOE$ 的圆心角是 $90^{\circ}$,半径是 $6m$,所以扇形 $AOE$ 的面积 $= \frac{90\pi \times 6^{2}}{360} = 9\pi(m^{2})$,扇形 $BCE$ 的圆心角是 $180^{\circ} - 120^{\circ} = 60^{\circ}$,半径是 $6 - 4 = 2(m)$,所以扇形 $BCE$ 的面积 $= \frac{60\pi \times 2^{2}}{360} = \frac{2}{3}\pi(m^{2})$,则小羊 $M$ 在草地上的最大活动区域的面积是 $9\pi + \frac{2}{3}\pi = \frac{29}{3}\pi(m^{2})$。故选 B。

5.「2025浙江绍兴期中」如图,边长为2的等边△ABC,将边BC不改变长度,变为⌢BC,得到以A为圆心,AB长为半径的扇形ABC,则此扇形的面积为
2
.

答案:答案 2
解析 由题意得 $l = 2$,$r = 2$,$\therefore S_{扇形} = \frac{1}{2}lr = \frac{1}{2} \times 2 \times 2 = 2$。
6.「2024江苏泰州二模」如图,在半径为2的圆形纸片中剪一个圆心角为60°的扇形(图中阴影部分),则该扇形的面积为______.

答案:答案 $2\pi$
解析 如图,过点 $O$ 作 $OD \perp AB$ 于 $D$,则 $AD = BD$,连接 $OA$,$\therefore OA = 2$,$\because \angle BAC = 60^{\circ}$,圆和扇形都是轴对称图形,且扇形内接于 $\odot O$,
$\therefore \angle OAD = \frac{1}{2}\angle BAC = 30^{\circ}$,

$\therefore OD = \frac{1}{2}OA = \frac{1}{2} \times 2 = 1$,
$\therefore AD = \sqrt{OA^{2} - OD^{2}} = \sqrt{2^{2} - 1^{2}} = \sqrt{3}$,
$\therefore AB = 2AD = 2\sqrt{3}$,
$\therefore$ 扇形的面积为 $\frac{60\pi \times (2\sqrt{3})^{2}}{360} = 2\pi$。
7.「2024江苏无锡中考」已知圆锥的底面圆半径为3,母线长为4,则圆锥的侧面积为(
B
)
A.6π
B.12π
C.15π
D.24π
答案:B $S_{侧} = \pi rl = \pi \times 3 \times 4 = 12\pi$。故选 B。
8.「2023山东东营中考」如果圆锥侧面展开图的面积是15π,母线长是5,则这个圆锥的底面半径是(
A
)
A.3
B.4
C.5
D.6
答案:A 设此圆锥的底面半径为 $R$,由题意得 $\pi R \times 5 = 15\pi$,$\therefore R = 3$。故选 A。
9.「2025江苏南通海门期末」若圆锥的底面半径为3,母线长为4,则这个圆锥的全面积为(
B
)
A.21
B.21π
C.12
D.12π
答案:B $\because$ 圆锥的底面半径为 $3$,$\therefore$ 圆锥的底面圆的周长为 $2\pi \times 3 = 6\pi$,又 $\because$ 母线长为 $4$,$\therefore$ 圆锥的全面积为 $\pi \times 3^{2} + \frac{1}{2} \times 6\pi \times 4 = 21\pi$。故选 B。
10.「2024广东广州中考」如图,圆锥的侧面展开图是一个圆心角为72°的扇形,若扇形的半径l是5,则该圆锥的体积是(
D
)

A.3√11/8π
B.√11/8π
C.2√6π
D.2√6/3π
答案:D 设圆锥的底面圆的半径为 $r$,则圆锥的底面圆的周长为 $2\pi r$,$\because$ 圆锥的侧面展开图是一个圆心角为 $72^{\circ}$ 的扇形,且扇形的半径 $l$ 是 $5$,$\therefore$ 扇形的弧长为 $\frac{72\pi \times 5}{180} = 2\pi$。$\because$ 圆锥的底面圆的周长与侧面展开图的弧长相等,$\therefore 2\pi r = 2\pi$,$\therefore r = 1$,$\therefore$ 圆锥的高为 $\sqrt{5^{2} - 1^{2}} = 2\sqrt{6}$。$\therefore$ 圆锥的体积为 $\frac{1}{3}\pi \times 1^{2} \times 2\sqrt{6} = \frac{2\sqrt{6}}{3}\pi$。故选 D。
11.「2024江苏宿迁中考」已知圆锥的底面半径为3,母线长为12,则其侧面展开扇形的圆心角的度数为
90
°.
答案:答案 90
解析 设圆锥的侧面展开扇形的圆心角的度数为 $n^{\circ}$,由题意得,$\frac{n\pi \times 12}{180} = 2\pi \times 3$,解得 $n = 90$。
12.新数学文化「2024湖北黄石港一模,★☆」《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺,问积及为米几何?”译文:屋内墙角处的米堆为一个圆锥的四分之一(如图),米堆底部的弧长为8尺,米堆的高为5尺,那么这个米堆遮挡的墙面面积为(
A
)

A.80/π平方尺
B.160/π平方尺
C.128/π平方尺
D.45π平方尺
答案:A 设米堆所在圆锥的底面圆的半径为 $r$ 尺,由米堆底部的弧长为 $8$ 尺,可得 $\frac{1}{4} \times 2\pi r = 8$,解得 $r = \frac{16}{\pi}$,$\therefore$ 这个米堆遮挡的墙面面积为 $2 \times \frac{1}{2} \times \frac{16}{\pi} \times 5 = \frac{80}{\pi}$ 平方尺。故选 A。