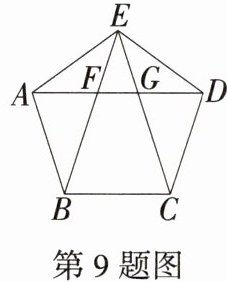
9. [2025 北京海淀期中,★☆]如图,正五边形的五个内角都相等,五条边都相等,连接对角线 AD,BE,CE,线段 AD 分别与 BE 和 CE 相交于点 F,G,下列结论:①$∠AGC= 108^{\circ }$;②$AG= AE$;③$∠EBC= 2∠BEC$;④$BF= DE$.其中正确结论的个数是(
D
)
A. 1
B. 2
C. 3
D. 4
答案:D ∵五边形 ABCDE 是正五边形,∴∠BAE = ∠AED = ∠CDE = 108°,AB = AE = DE = CD,∴∠ABE = ∠AEB = ∠EAD = ∠ADE = ∠CED = 36°,∴∠AGC = ∠DGE = 180° - ∠EDA - ∠CED = 108°,故①正确;∵∠AGE = 180° - 108° = 72°,∠AEG = 180° - 36° - 72° = 72°,∴∠AEG = ∠AGE,∴AE = AG,故②正确;∵∠ABC = ∠DCB = 108°,∠ABE = ∠DCE = 36°,∴∠EBC = ∠ECB = 108° - 36° = 72°,∴∠BEC = 180° - 72° - 72° = 36°,∴∠EBC = 2∠BEC,故③正确;∵∠ABE = 36°,∠BAF = 108° - 36° = 72°,∴∠BFA = 180° - 72° - 36° = 72°,∴∠BAF = ∠BFA,∴AB = BF,∵AB = DE,∴BF = DE,故④正确。故选 D。
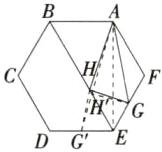
10. [2024 四川绵阳中考,★☆]如图,在边长为 2 的正六边形 ABCDEF 中,连接 BE,点 H 在 BE 上运动,点 G 为 EF 的中点,当△AGH 的周长最小时,$AH+GH= $( )

A. $2\sqrt {3}$
B. $\sqrt {13}$
C. 12
D. 13
答案:B 如图,要使△AGH 的周长最小,则需使 AH + HG 的值最小,利用正六边形的性质可得点 G 关于直线 BE 的对称点 G'为 DE 的中点,由对称性可得 HG' = HG,∴当 A、H、G'三点共线时 AH + HG 的值最小,最小值为 AG'的长,设此时 AG'交 BE 于点 H',连接 AE,H'G,易知∠F = 120°,AF = EF = 2,∴AE = $2\sqrt{3}$,∠AEF = 30°,∴∠AEG' = 90°,∵G'为 DE 的中点,∴EG' = $\frac{1}{2}$DE = 1,∴AG' = $\sqrt{1² + (2\sqrt{3})²}$ = $\sqrt{13}$,故当△AGH 的周长最小时,AH + GH = $\sqrt{13}$。故选 B。
11. 学科特色方程思想 [2022 四川遂宁中考,★☆]如图,正六边形 ABCDEF 的顶点 A、F 分别在正方形 BMGH 的边 BH、GH 上.若正方形 BMGH 的边长为 6,则正六边形 ABCDEF 的边长为____
4
.
答案:答案 4
解析 设 AF = x,则 AB = x,AH = 6 - x,∵六边形 ABCDEF 是正六边形,∴∠BAF = $\frac{(6 - 2)×180°}{6}$ = 120°,∴∠HAF = 60°,∵∠AHF = 90°,∴∠AFH = 30°,∴AF = 2AH,∴x = 2(6 - x),解得 x = 4,∴AB = 4,即正六边形 ABCDEF 的边长为 4。
12. [2025 河北沧州期中,★☆]如图,已知五边形 ABCDE 是⊙O 的内接正五边形,点 I 是△ABC 的内心,则$∠CIA-∠AOB= $
72°
.

答案:答案 72°
解析 ∵五边形 ABCDE 是⊙O 的内接正五边形,∴∠AOB = 360°÷5 = 72°,∵正五边形 ABCDE 的内角和为 (5 - 2)×180° = 3×180° = 540°,∴∠ABC = $\frac{540°}{5}$ = 108°。∵AB = BC,∴∠CAB = ∠ACB = $\frac{180° - ∠ABC}{2}$ = 36°,∵点 I 为△ABC 的内心,∴AI 平分∠CAB,CI 平分∠ACB,∴∠CAI = ∠ACI = 18°,∴∠CIA = 180° - ∠CAI - ∠ACI = 180° - 18° - 18° = 144°,∴∠CIA - ∠AOB = 144° - 72° = 72°。
13. [2023 浙江杭州中考,★☆]如图,六边形 ABCDEF 是⊙O 的内接正六边形,设正六边形 ABCDEF 的面积为$S_{1}$,△ACE 的面积为$S_{2}$,则$\frac {S_{1}}{S_{2}}= $____.

答案:答案 2
解析 如图,连接 OA,OC,OE。

∵六边形 ABCDEF 是⊙O 的内接正六边形,∴AC = AE = CE,∴△ACE 是⊙O 的内接正三角形,∵∠B = 120°,AB = BC,∴∠BAC = ∠BCA = $\frac{1}{2}$(180° - ∠B) = 30°,∵∠CAE = 60°,∴∠OAC = ∠OAE = 30°,∴∠BAC = ∠OAC = 30°,同理可得∠BCA = ∠OCA = 30°,又∵AC = AC,∴△BAC ≌ △OAC(ASA),∴$S_{△BAC}$ = $S_{△AOC}$,由圆和正六边形的性质可得 $S_{△BAC}$ = $S_{△AFE}$ = $S_{△CDE}$,由圆和正三角形的性质可得 $S_{△OAC}$ = $S_{△OAE}$ = $S_{△OCE}$,∵$S_1$ = $S_{△BAC}$ + $S_{△AEF}$ + $S_{△CDE}$ + $S_{△OAC}$ + $S_{△OAE}$ + $S_{△OCE}$ = 2($S_{△OAC}$ + $S_{△OAE}$ + $S_{△OCE}$) = $2S_2$,∴$\frac{S_1}{S_2}$ = 2。
14. [2024 福建莆田二十五中期中,★☆]如图,正方形 ABCD 内接于⊙O,E 是$\overset{\frown }{BC}$的中点,连接 AE,DE,CE.
(1)求证:$AE= DE$.
(2)求证:$AE+CE= \sqrt {2}DE$.

答案:证明 (1)∵四边形 ABCD 是正方形,∴AB = CD,∴$\overset{\frown}{AB}$ = $\overset{\frown}{CD}$。∵E 是$\overset{\frown}{BC}$的中点,∴$\overset{\frown}{BE}$ = $\overset{\frown}{EC}$。∴$\overset{\frown}{AE}$ = $\overset{\frown}{DE}$,∴AE = DE。
(2)连接 BD,过点 D 作 DF⊥DE 交 EC 的延长线于 F。

∵四边形 ABCD 是正方形,∴∠DBC = ∠DEC = 45°,DA = DC,∵∠EDF = 90°,∴∠F = 90° - 45° = 45°,∴DE = DF。∵∠ADC = ∠EDF = 90°,∴∠ADE = ∠CDF。∵AD = CD,∴$\overset{\frown}{AD}$ = $\overset{\frown}{CD}$,∴∠AED = ∠DEC = 45°,∴∠AED = ∠F = 45°。在△ADE 和△CDF 中,
$\begin{cases}∠AED = ∠F, \\∠ADE = ∠CDF, \\DA = DC,\end{cases}$
∴△ADE ≌ △CDF(AAS),∴AE = CF,∴EF = $\sqrt{2}$DE = EC + CF = EC + AE,即 AE + CE = $\sqrt{2}$DE。
15. 新课标几何直观 [2025 河北石家庄桥西期末]如图,正六边形 ABCDEF 的边长为 2,点 G 为 DE 边上一点,连接 AG,FG,CG,则△AFG 与△CDG 的面积和为( )

A. 4
B. $3\sqrt {3}$
C. $2\sqrt {3}$
D. 随点 G 位置而变化
答案:C 如图,过点 G 作 AF 的垂线,分别交 AF,CD 的延长线于点 M,N,设正六边形的中心为 O,过点 O 作 AF 的垂线,分别交 AF,CD 于点 P,Q,则 MN = PQ,连接 OC,在 Rt△COQ 中,易知 OC = 2,CQ = 1,∴OQ = $\sqrt{OC² - CQ²}$ = $\sqrt{3}$,∴MN = PQ = $2\sqrt{3}$,∴$S_{△AFG}$ + $S_{△CDG}$ = $\frac{1}{2}$AF·GM + $\frac{1}{2}$CD·GN = $\frac{1}{2}$×2×GM + $\frac{1}{2}$×2×GN = GM + GN = MN = $2\sqrt{3}$。故选 C。

16. 新课标推理能力 [2025 江苏南京秦淮期末]如图,点 O 是边长为 6 的正六边形 ABCDEF 和边长为 a 的正方形 MNPQ 的中心,将正方形 MNPQ 绕点 O 旋转一周.若在旋转过程中,正方形 MNPQ 始终在正六边形 ABCDEF 的内部(即正方形边上的所有点都在正六边形内),则 a 的取值范围是____.

答案:答案 0 < a < $3\sqrt{6}$
解析 如图,当正方形 MNPQ 的一个顶点 Q 在 EF 的中点时,正方形 MNPQ 的边长最大,连接 OE,OF,OQ,OP,则 OQ⊥EF,∵六边形 ABCDEF 是正六边形,中心为 O,∴∠EOF = $\frac{360°}{6}$ = 60°,OE = OF,∴△EOF 是正三角形,∴OE = OF = EF = 6,QE = QF = 3,在 Rt△EOQ 中,OQ = $\sqrt{OE² - EQ²}$ = $3\sqrt{3}$,在 Rt△POQ 中,OP = OQ = $3\sqrt{3}$,∴PQ = $\sqrt{OP² + OQ²}$ = $3\sqrt{6}$,即正方形 MNPQ 的边长最大为 $3\sqrt{6}$,∴a 的取值范围是 0 < a < $3\sqrt{6}$。
