10.「2025江苏镇江期中,★☆」如图,在$Rt\triangle ABC$中,$\angle C= 90^{\circ}$,AC= 3,BC= 4,P为边BC上一点,以P为圆心,$\frac{7}{2}$为半径作圆,则当点C在圆内,点A在圆外时,线段CP的取值范围为(
$\frac{\sqrt{13}}{2} < CP < \frac{7}{2}$
)
A.$\frac{\sqrt{13}}{2}<CP<\frac{7}{2}$
B.$0<CP<\frac{7}{2}$
C.$3<CP<5$
D.$\frac{1}{2}<CP<\frac{5}{2}$
答案:A 当点C在⊙P内时,CP < $\frac{7}{2}$,当点A在⊙P上时,PA = $\frac{7}{2}$,∵∠C = 90°,AC = 3,∴此时CP = $\sqrt{PA^2 - AC^2} = \sqrt{(\frac{7}{2})^2 - 3^2} = \frac{\sqrt{13}}{2}$,∴要使点A在⊙P外,则CP > $\frac{\sqrt{13}}{2}$,∴满足条件的线段CP的取值范围为 $\frac{\sqrt{13}}{2} < CP < \frac{7}{2}$。故选A。
11.「★☆」平面内一点P到$\odot O$上一点的最小距离为3 cm,最大距离为7 cm,则$\odot O$的半径为
2 cm 或 5 cm
.
答案:答案 2 cm 或 5 cm
解析 设P到圆心O的距离为d,⊙O的半径为r,当点P在⊙O内时,点P到⊙O上一点的最小距离为r - d = 3 cm,最大距离为r + d = 7 cm,∴2r = 10 cm,∴r = 5 cm。当点P在⊙O外时,点P到⊙O上一点的最小距离为d - r = 3 cm,最大距离为d + r = 7 cm,∴2r = 4 cm,∴r = 2 cm。综上,⊙O的半径为2 cm 或 5 cm。
方法解读 点到圆上一点距离最值问题
设该点到圆心的距离为d,圆的半径为r,则平面内一点到圆上一点距离的最大值为d + r,最小值为 |d - r|。该结论常用在解决动点在圆上的线段最值问题。
初中阶段所学线段最值相关结论简单概述有:两点之间线段最短;垂线段最短;点到圆上一点最小值为 |d - r|。
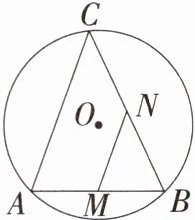
12.「2025浙江宁波期中,★☆」如图,AB是$\odot O$的弦,C是优弧$\overparen{AB}$上一动点,连接AC,BC,M,N分别是AB,BC的中点,连接MN.若AB= 8,$\angle ACB= 45^{\circ}$,则MN的最大值为____.
答案:答案 $4\sqrt{2}$
解析 ∵点M,N分别是AB,BC的中点,∴MN = $\frac{1}{2}AC$,∴当AC取得最大值时,MN就取得最大值,当AC取得最大值时,AC为⊙O的直径。如图,∵AC是⊙O的直径,∴∠ABC = 90°,∵∠ACB = 45°,∴∠CAB = 45°,∴AB = CB,∵AB = 8,∴AC = $8\sqrt{2}$,∴MN = $\frac{1}{2}AC = 4\sqrt{2}$。故MN的最大值为 $4\sqrt{2}$。

13.「2025吉林长春榆树期末,★☆」如图,AB是半圆O的直径,C是半圆弧的中点,$\triangle ABD和\triangle ABC$均内接于半圆O,AC、OC分别交BD于点E、F.若D是$\overparen{AC}$的中点,给出下面四个结论:①$\angle CAD= \angle DBA$;②CE= CF;③BC= 2AD;④$AD^{2}+DF^{2}= BF^{2}$.其中正确结论的序号是____.

答案:答案 ①②④
解析 ①∵点D是 $\overset{\frown}{AC}$ 的中点,∴$\overset{\frown}{AD} = \overset{\frown}{CD}$,∴∠CAD = ∠DBA,故①正确;
②∵AB是半圆的直径,∴∠ADB = 90°,∴∠DAE + ∠AED = 90°,∵C是半圆弧的中点,∴CO⊥AB,∴∠COB = 90°,∴∠OBF + ∠BFO = 90°,∴∠AED = ∠BFO,∴∠CEF = ∠CFE,∴CE = CF,故②正确;
③如图,连接CD,∵点D是 $\overset{\frown}{AC}$ 的中点,点C是 $\overset{\frown}{AB}$ 的中点,∴$\overset{\frown}{CD} = \overset{\frown}{AD}$,$\overset{\frown}{AC} = \overset{\frown}{BC}$,∴CD = AD,AC = BC,∵AD + CD > AC,∴2AD > AC,∴2AD > BC,故③错误;

④如图,连接AF,∵C是半圆弧的中点,∴CO垂直平分AB,∴FA = FB,在Rt△ADF中,由勾股定理得 $AD^2 + DF^2 = AF^2$,∴$AD^2 + DF^2 = BF^2$,故④正确。
综上所述,正确结论的序号是①②④。
14.「2024安徽中考,★☆」如图,$\odot O是\triangle ABC$的外接圆,D是直径AB上一点,$\angle ACD$的平分线交AB于点E,交$\odot O$于另一点F,FA= FE.
(1)求证:CD⊥AB.
(2)设FM⊥AB,垂足为M,若OM= OE= 1,求AC的长.
$4\sqrt{2}$

答案:解析 (1)证明:∵FA = FE,∴∠FAE = ∠AEF,∵∠FAE与∠BCE都是 $\overset{\frown}{BF}$ 所对的圆周角,∴∠FAE = ∠BCE,∵∠AEF = ∠CEB,∴∠CEB = ∠BCE,∵CE平分∠ACD,∴∠ACE = ∠DCE。∵AB是直径,∴∠ACB = 90°,∴∠CEB + ∠DCE = ∠BCE + ∠ACE = ∠ACB = 90°,∴∠CDE = 90°,∴CD⊥AB。
(2)由(1)知,∠BEC = ∠BCE,∴BE = BC,∵FA = FE,FM⊥AB,∴MA = ME = OM + OE = 2,∴AE = 4,∴圆的半径OA = OB = AE - OE = 3,∴BC = BE = OB - OE = 2,在Rt△ABC中,AB = 6,BC = 2,∠ACB = 90°,∴AC = $\sqrt{AB^2 - BC^2} = \sqrt{6^2 - 2^2} = 4\sqrt{2}$。
15.「★☆」如图,抛物线$y= \frac{1}{4}x^{2}-4$与x轴交于A,B两点,P是以点C(0,3)为圆心,2为半径的圆上的动点,Q是线段PA的中点,连接OQ,则线段OQ的最大值为( )

A.3
B.$\frac{\sqrt{41}}{2}$
C.$\frac{7}{2}$
D.4
答案:C 如图,连接BP,当y = 0时,$\frac{1}{4}x^2 - 4 = 0$,解得 $x_1 = 4$,$x_2 = -4$,∴A(-4,0),B(4,0)。∵Q是线段PA的中点,∴OQ为△ABP的中位线,∴OQ = $\frac{1}{2}BP$。∴当BP的值最大时,OQ的值最大,当BP过圆心C时,BP的值最大。如图,当点P运动到P'的位置时,BP的值最大。∵BC = $\sqrt{3^2 + 4^2} = 5$,∴BP' = 5 + 2 = 7,∴线段OQ的最大值是 $\frac{7}{2}$。故选C。
