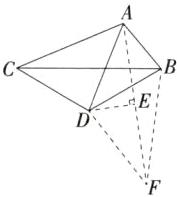
4.如图,$△ABC$为等边三角形,以$AB为边向外作△ABD$,使$∠ADB= 120°$,再以点$C为旋转中心把△CBD旋转到△CAE$,则下列结论:
①$D$,$A$,$E$三点共线;②$DC平分∠BDA$;③$∠E= ∠BAC$;④$DC= DB+DA$。
其中正确的有(
)
A.4个
B.3个
C.2个
D.1个
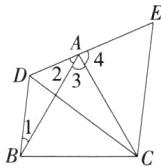
答案:A 如图,①设∠1=$x^{\circ}$,则∠2=(60−$x$)°,∠DBC=($x$+60)°,故∠4=($x$+60)°,∴∠2+∠3+∠4=(60−$x$)°+60°+($x$+60)°=180°,∴D,A,E三点共线,故①正确;
②∵△BCD绕着点C按顺时针方向旋转60°得到△ACE,∴CE=CD,∠DCE=60°,∠BDC=∠E,∴△CDE为等边三角形,∴∠CDA=∠E=60°,∴∠ADC=∠BDC=60°,∴DC平分∠BDA,故②正确;
③由题易知∠BAC=60°,∠E=60°,∴∠E=∠BAC,故③正确;
④由旋转的性质可知AE=DB,∵△CDE为等边三角形,∴DC=DE=AE+AD=DB+DA,故④正确。
综上,正确的有4个。
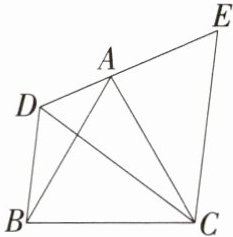
5.如图,已知四边形$ABCD$的对角互补,且$∠BAC= ∠DAC$,$AB= 15$,$AD= 12$。过顶点$C作CE⊥AB于E$,则$\frac{AE}{BE}$的值为( )

A.9
B.$\sqrt{73}$
C.7.2
D.6
答案:A 如图,过点C作CF⊥AD交AD的延长线于点F,则∠CFD=90°,∵CE⊥AB,∴∠CEB=90°,∴∠CEB=∠CFD。∵∠BAC=∠DAC,∴AC平分∠BAD,∴CE=CF。∵四边形ABCD的对角互补,∴∠B+∠ADC=180°。∵∠CDF+∠ADC=180°,∴∠B=∠CDF,在△CEB和△CFD中,$\begin{cases}∠CEB=∠F\\∠B=∠CDF\\CE=CF\end{cases}$,∴△CEB≌△CFD(AAS),∴BE=DF,在Rt△ACE和Rt△ACF中,$\begin{cases}AC=AC\\CE=CF\end{cases}$,∴Rt△ACE≌Rt△ACF(HL),∴AE=AF。设BE=DF=$a$,∵AB=15,AD=12,AB=AE+EB=AF+EB,∴15=12+$a$+$a$,∴$a$=1.5,∴AE=15−$a$=15−1.5=13.5,BE=$a$=1.5,∴$\frac{AE}{BE}$=$\frac{13.5}{1.5}$=9,故选A。

6.方程思想如图,已知正方形$ABCD$的边长为3,点$E$,$F分别是AB$,$BC$边上的点,且$∠EDF= 45°$,将$△ADE绕点D逆时针旋转90°得到△CDM$。若$AE= 1$,则$MF$的长为
$\frac{5}{2}$
。
答案:答案 $\frac{5}{2}$
解析 由旋转的性质可得∠A=∠DCM=90°,DE=DM,∴∠FCM=∠FCD+∠DCM=180°,∴F,C,M三点共线。由题意得∠EDM=90°,即∠EDF+∠FDM=90°。∵∠EDF=45°,∴∠FDM=∠EDF=45°。在△DEF和△DMF中,$\begin{cases}DE=DM\\∠EDF=∠MDF\\DF=DF\end{cases}$,∴△DEF≌△DMF(SAS),∴EF=MF。设EF=MF=$x$,∵AE=CM=1,且BC=3,∴BM=BC+CM=3+1=4,∴BF=BM−MF=4−$x$,∵EB=AB−AE=3−1=2,∴在Rt△EBF中,由勾股定理得EB²+BF²=EF²,即2²+(4−$x$)²=$x$²,解得$x$=$\frac{5}{2}$,∴MF=$\frac{5}{2}$。
7.如图,在$△ABC$中,$∠BAC= 90°$,$AB= AC$,点$D$,$E都在BC$上,$∠DAE= 45°$,$BD= 3$,$CE= 5$,则$DE$的长为____。

答案:答案 $\sqrt{34}$
解析 将△ABD绕点A逆时针旋转至△ACD',使得AB与AC重合,如图所示,连接ED',
∵∠BAC=90°,AB=AC,∴∠B=∠ACB=45°,由旋转的性质可知△ABD≌△ACD',∴CD'=BD=3,∠ACD'=∠B=45°,∴∠D'CE=∠ACD'+∠ACB=90°,∵CE=5,∴D'E=$\sqrt{EC^{2}+D'C^{2}}$=$\sqrt{34}$,由旋转的性质可知∠BAD=∠CAD',∴∠BAC=∠BAD+∠DAC=∠CAD'+∠DAC=90°,即∠DAD'=90°,又∵∠DAE=45°,∴∠D'AE=45°,∴∠DAE=∠D'AE,又AD=AD',AE=AE,∴△ADE≌△AD'E(SAS),∴DE=D'E=$\sqrt{34}$。

8.如图所示,$△ABC$是边长为1的等边三角形,$△BDC是顶角∠BDC为120°$的等腰三角形,以$D为顶点作∠MDN= 60°$,点$M$,$N分别在AB$,$AC$上,则$△AMN$的周长为____。

答案:答案 2
解析 如图,延长AC至E,使得CE=BM,连接DE。∵△ABC是等边三角形,且△BDC是顶角∠BDC为120°的等腰三角形,∴∠ABC=∠ACB=60°,∠DBC=∠DCB=30°,则∠ABD=∠DCE=90°,在△MBD和△ECD中,$\begin{cases}BM=CE\\∠MBD=∠DCE\\BD=CD\end{cases}$,∴△MBD≌△ECD(SAS),∴MD=ED,∠MDB=∠EDC,∵∠MDN=60°,∠BDC=120°,∴∠MDB+∠NDC=60°,∴∠EDC+∠NDC=60°,即∠EDN=60°=∠MDN,在△MDN和△EDN中,$\begin{cases}MD=ED\\∠MDN=∠EDN\\DN=DN\end{cases}$,∴△MDN≌△EDN(SAS),∴MN=EN,即MN=NC+CE=NC+BM,∴△AMN的周长=AM+MN+AN=AM+BM+NC+AN=AB+AC=2。