1.「2025北京西城期中」下列关于抛物线$y= -x^{2}+2$的说法正确的是(
D
)
A.抛物线开口向上
B.$x>0$时,$y随x$的增大而增大
C.顶点坐标为$(-1,2)$
D.当$x = 0$时,$y$有最大值,是2
答案:D ∵抛物线y=−x²+2,∴抛物线对称轴为y轴,开口向下,顶点坐标为(0,2),∴在对称轴的右侧,y随x的增大而减小,∴当x=0时,y有最大值,是2,故A、B、C选项错误,D选项正确。故选D。
2.「2024湖北武汉期末」抛物线$y= -x^{2}+1与y= x^{2}+1$相同的性质是(
D
)
A.开口向上
B.对称轴是$x$轴
C.有最低点
D.经过点$(0,1)$
答案:D A项,抛物线y=−x²+1的开口向下,抛物线y=x²+1的开口向上,不合题意;B项,两抛物线的对称轴均是y轴,不合题意;C项,抛物线y=x²+1有最低点,抛物线y=−x²+1有最高点,不合题意;D项,两抛物线都经过点(0,1),符合题意。故选D。
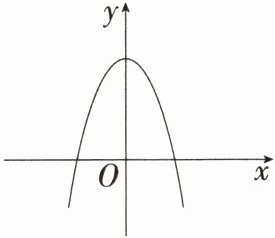
3.「2025河南商丘月考」已知二次函数$y = ax^{2}+k$的图象如图所示,则$a$,$k$的符号正确的是(
C
)
A.$a>0$,$k>0$
B.$a>0$,$k<0$
C.$a<0$,$k>0$
D.$a<0$,$k<0$
答案:C ∵二次函数y=ax²+k的图象开口向下,顶点在y轴正半轴上,∴a<0,k>0。故选C。
4.「2025河南漯河月考」已知点$A(-2,y_{1})$,$B(1,y_{2})$,$C(5,y_{3})在二次函数y= -3x^{2}+k$的图象上,则$y_{1}$,$y_{2}$,$y_{3}$的大小关系是(
C
)
A.$y_{1}<y_{2}<y_{3}$
B.$y_{3}<y_{2}<y_{1}$
C.$y_{3}<y_{1}<y_{2}$
D.$y_{1}<y_{3}<y_{2}$
答案:C 由二次函数图象的性质可知点A(−2,y₁)关于对称轴x=0的对称点为(2,y₁),∵−3<0,∴当x>0时,y随x的增大而减小,∵1<2<5,∴y₃<y₁<y₂。故选C。
5.「2025上海闵行月考」已知抛物线$y= x^{2}+2$,把抛物线向上平移
3
个单位后,能使得平移后的抛物线与$y轴的公共点的坐标为(0,5)$。
答案:答案 3
解析 设向上平移m个单位,则平移后的抛物线的解析式为y=x²+2+m,把(0,5)代入,得5=2+m,∴m=3。
6.学科易错题「2025青海西宁城西月考」把抛物线$y= -2x^{2}$沿y轴平移3个单位长度,所得抛物线的解析式为
y=-2x²+3或y=-2x²-3
。
答案:答案 y=−2x²+3或y=−2x²−3
解析 ∵函数图象平移的规律为“上加下减常数项”,∴抛物线y=−2x²沿y轴正方向平移时,平移后的抛物线的解析式为y=−2x²+3,抛物线y=−2x²沿y轴负方向平移时,平移后的抛物线的解析式为y=−2x²−3。
易错点 忽视平移的方向导致漏解。
7.「2025辽宁营口期中改编,★☆」在同一直角坐标系中,一次函数$y = ax + c$和二次函数$y = ax^{2}+c$的图象大致为(
B
)

答案:B A. 由二次函数图象得a<0,由一次函数图象得a>0,矛盾,不符合题意;B. 由二次函数图象得a<0,由一次函数图象得a<0,都过点(0,c),一致,符合题意;C. 由二次函数图象得a>0,由一次函数图象得a<0,矛盾,不符合题意;D. 由二次函数图象得a>0,c<0,由一次函数图象得a>0,c>0,矛盾,不符合题意。故选B。
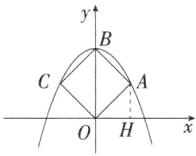
8.「2025广东广州番禺一模,★☆」如图,抛物线$y = ax^{2}+c经过正方形OABC的三个顶点A$,$B$,$C$,点$B在y$轴上,则$ac$的值为( )

A.$-1$
B.$-2$
C.$-3$
D.$-4$
答案:B 如图,过点A作AH⊥x轴于H,∵四边形ABCO是正方形,∴∠AOB = 45°,∴∠AOH = 45°,∴AH = OH,设A(m,m),则B(0,2m),∴{m = am² + c, 2m = c},解得{a = -1/m, c = 2m},∴ac的值为 -2,故选B。
9.「2024黑龙江大庆期中,★☆」如图,两条抛物线$y_{1}= -\frac{1}{2}x^{2}+1$,$y_{2}= -\frac{1}{2}x^{2}-1与分别经过点(-2,0)$,$(2,0)且平行于y$轴的两条平行线围成的阴影部分的面积为______。

答案:答案 8
解析 如图,过抛物线y₂ = -1/2x² - 1的顶点(0,-1)的平行于x轴的直线与抛物线y₁ = -1/2x² + 1围成的图形的形状,和过点(0,-3)的平行于x轴的直线与抛物线y₂ = -1/2x² - 1围成的图形的形状相同,故把直线y = -1上方的阴影部分向下平移2个单位即可与直线y = -1下方的阴影部分拼成一个长为4,宽为2的矩形,因此阴影部分的面积 = 矩形的面积 = 4×2 = 8。

10.「2024重庆铜梁月考,★☆」如图,正方形$ABCD的顶点C$、$D在x$轴上,$A$、$B恰好在二次函数y = x^{2}-3$的图象上,则图中阴影部分的面积之和为______
18
。

答案:答案 18
解析 ∵抛物线y = x² - 3和正方形ABCD都是轴对称图形,且它们的对称轴均为y轴,∴OD = OC = 1/2BC,S阴影 = S矩形BCOE。设点B的坐标为(n,2n)(n > 0),∵点B在二次函数y = x² - 3的图象上,∴2n = n² - 3,解得n₁ = 3,n₂ = -1(舍去),∴点B的坐标为(3,6),∴S阴影 = S矩形BCOE = 3×6 = 18。