1.「2025 云南昆明期中」若二次函数$y= ax^{2}的图象经过点A(3,-6)$,则该图象必经过点 (
B
)
A.$(-3,6)$
B.$(-3,-6)$
C.$(6,-3)$
D.$(6,3)$
答案:B ∵ 二次函数 y = ax² 的图象关于 y 轴对称,A(3, -6) 关于 y 轴对称的点为 (-3, -6),∴ 该图象必过点 (-3, -6)。故选 B。
2.「2025 江西新余模拟」若$y= (m-1)x^{m^{2}-2}$是二次函数,且图象开口向上,则 m 的值为 (
C
)
A.$\pm 2$
B.0
C.2
D.-2
答案:C ∵$ y = (m - 1)x^(m² - 2) $是二次函数,∴ m² - 2 = 2,得 m = -2 或 2,又 ∵ 图象的开口向上,∴ m - 1 > 0,即 m > 1,∴ m = 2。故选 C。
3.「2025 天津河西月考」抛物线$y= 4x^{2},y= -4x^{2},y= \frac {1}{2}x^{2}$共有的性质是 (
B
)
A.对称轴是 x 轴
B.对称轴是 y 轴
C.都有最高点
D.y 随 x 的增大而增大
答案:B 抛物线 y = 4x²,y = -4x²,y = 1/2x² 共有的性质是顶点坐标都是 (0, 0),对称轴都是 y 轴,故选项 B 符合题意。故选 B。
4.「2024 广东中考」若点$(0,y_{1}),(1,y_{2}),(2,y_{3})都在二次函数y= x^{2}$的图象上,则 (
A
)
A.$y_{3}>y_{2}>y_{1}$
B.$y_{2}>y_{1}>y_{3}$
C.$y_{1}>y_{3}>y_{2}$
D.$y_{3}>y_{1}>y_{2}$
答案:A 在二次函数 y = x² 中,图象开口向上,且对称轴为 y 轴,∴ 当 x ≥ 0 时,y 随 x 的增大而增大,∵ 2 > 1 > 0,∴ y₃ > y₂ > y₁。故选 A。
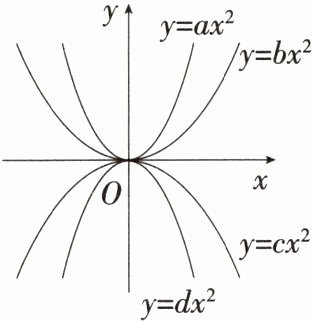
5.「2025 福建福州月考」如图所示的是四个二次函数的图象,则 a、b、c、d 的大小关系为 (
B
)
A.$d\lt c\lt a\lt b$
B.$d\lt c\lt b\lt a$
C.$c\lt d\lt a\lt b$
D.$c\lt d\lt b\lt a$
答案:B 因为直线 x = 1 与四条抛物线的交点从上到下依次为 (1, a),(1, b),(1, c),(1, d),所以 d < c < b < a。故选 B。
6.「2025 青海西宁城西月考」已知二次函数$y= 2025x^{2}的图象上有两个不同点P(t_{1},\frac {1}{4}),Q(t_{2},\frac {1}{4})$,则$t_{1}+t_{2}= $
0
.
答案:答案 0
解析 ∵ P(t₁, 1/4),Q(t₂, 1/4),∴ 点 P、Q 的纵坐标相等,∵ 二次函数 y = 2025x² 的图象关于 y 轴对称,∴ 点 P、Q 关于 y 轴对称,∴ t₁ + t₂ = 0。
7.如图,正方形 ABCD 的边长为 4,以正方形的中心 O 为原点建立平面直角坐标系,作出函数$y= 2x^{2}与y= -2x^{2}$的图象,则阴影部分的面积

是
8
.
答案:答案 8
解析 由题意知函数 y = 2x² 与 y = -2x² 的图象关于 x 轴对称,∴ 题图中阴影部分的面积是题图中正方形 ABCD 面积的一半,∴ S阴 = 1/2 × 4² = 8。
8.「2023 河南周口鹿邑月考」
(1)在同一直角坐标系中,画出二次函数$y= \frac {1}{2}x^{2}和y= -\frac {1}{2}x^{2}$的图象.
(2)从函数图象的形状、开口方向、对称轴、顶点坐标等方面说出两个函数图象的相同点与不同点.

答案:解析 (1) 二次函数 y = 1/2x² 和 y = -1/2x² 的图象如图所示。

(2) 相同点:形状都是抛物线,对称轴都是 y 轴,顶点坐标都是 (0, 0);
不同点:y = 1/2x² 的图象开口向上,y = -1/2x² 的图象开口向下。
9.学科多解法「2025 河南郑州金水期中,★☆」点$(-1,y_{1}),(-\frac {1}{2},y_{2}),(2,y_{3})都在二次函数y= -x^{2}$的图象上,则$y_{1},y_{2},y_{3}$的大小关系为 (
C
)
A.$y_{3}>y_{2}>y_{1}$
B.$y_{1}>y_{2}>y_{3}$
C.$y_{2}>y_{1}>y_{3}$
D.$y_{2}>y_{3}>y_{1}$
答案:【解法一】图象性质法:二次函数 y = -x² 的图象开口向下,对称轴为直线 x = 0,∴ 当 x < 0 时,y 随 x 的增大而增大,∵ 点 (2, y₃) 关于直线 x = 0 的对称点为 (-2, y₃),-1/2 > -1 > -2,∴ y₂ > y₁ > y₃。故选 C。
【解法二】代入求值法:∵ (-1, y₁),(-1/2, y₂),(2, y₃) 都在二次函数 y = -x² 的图象上,则 y₁ = -(-1)² = -1,y₂ = -(-1/2)² = -1/4,y₃ = -2² = -4,∴ y₂ > y₁ > y₃。故选 C。
【解法三】距离法:抛物线的对称轴为直线 x = 0,则三个点离对称轴的距离依次为 1,1/2,2,∵ 二次项系数 a = -1 < 0,∴ 离对称轴的距离越大,对应的函数值越小,故 y₂ > y₁ > y₃。故选 C。